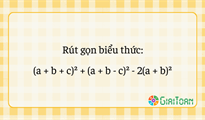Tính a³ + b³ Những hằng đẳng thức đáng nhớ

15 Đánh giá

a³ + b³

A. Hằng đẳng thức số 6
B. Tổng hai lập phương
C. Bài tập tự luyện

Bảy hằng đẳng thức đáng nhớ đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh lớp 8 ôn tập và củng cố kiến thức về dạng toán về những hằng đẳng thức đáng nhớ. Tài liệu bao gồm công thức hằng đẳng thức, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề hằng đẳng thức Toán lớp 8. Chúc các bạn học tập hiệu quả!

A. Hằng đẳng thức số 6

Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó.

A³ + B³ = (A + B)(A² - AB + B²)

Chứng minh hằng đẳng thức

A³ + B³ = (A + B)(A² - AB + B²)

Xét vế phải của hằng đẳng thức

VP = (A + B)(A² - AB + B²)

VP = A³ - A²B + AB² + A²B – AB²+ B³

VP = A³ + (-A²B + A²B) +( AB²– AB²) + B³

VP = A³+ B³ = VT => điều phải chứng minh

B. Tổng hai lập phương

Ví dụ: Viết các biểu thức sau dưới dạng tích:

a) x³ + 125

b) b³ + 8a³

Hướng dẫn giải

a) Ta có: x³ + 125

= x³ + 5³

= (x + 5)(x² - 5x + 5²)

= (x + 5)(x² - 5x + 25)

b) Ta có: b³ + 8a³

= b³ + (2a)³

= (b + 2a)[b² - 2ab + (2a)²]

= (b + 2a)[b² - 2ab + 4a²]

Ví dụ: Tính giá trị của biểu thức a³ + b³biết a + b = 2 và ab = -1

Hướng dẫn giải

Ta có:

$\begin{matrix} {a^3} + {b^3} \hfill \\ = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) \hfill \\ = \left( {a + b} \right)\left[ {{a^2} + 2ab + {b^2} - 2ab - ab} \right] \hfill \\ = \left( {a + b} \right)\left[ {\left( {{a^2} + 2ab + {b^2}} \right) - 3ab} \right] \hfill \\ = \left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - 3ab} \right]\left( * \right) \hfill \\ \end{matrix}$

Thay a + b = 2 và ab = -1 vào (*) ta được:

$\left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - 3ab} \right] = 2.\left[ {{2^2} - 3.\left( { - 1} \right)} \right] = 2.\left[ {4 + 3} \right] = 14$

C. Bài tập tự luyện

Bài 1: Viết các đa thức sau thành tích của hai đa thức khác:

a) x³ + 8

b) 8x³ + 1

c) (2x - y)³ + y³

Bài 2: Cho x³ + y³ = 30 và x² - xy + y² = 10. Tính x + y.

Bài 3: Tính giá trị của biểu thức:

a) A = (x + 3)(x² - 3x + 9) tại x = 10

b) B = (3x + 2)(9x² - 6x + 4) tại x = 1

----------------------------------------------------

Hi vọng Chuyên đề Hằng đẳng thức đáng nhớ là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình lớp 8 cũng như ôn luyện cho các kì thi sắp tới. Chúc các bạn học tốt!