Giaitoan.com Toán 8

Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức Phân tích đa thức thành nhân tử

Nội dung Tải về
  • 18 Đánh giá

Cách phân tích đa thức thành nhân tử

Bài tập Toán 8: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức là tài liệu ôn tập với các bài tập Toán 8 phân tích đa thức thành nhân tử, giúp các bạn học sinh học tốt Toán 8 và luyện tập các dạng Toán lớp 8 đạt kết quả tốt nhất, góp phần củng cố thêm kiến thức của các bạn học sinh.

A. 7 hằng đẳng thức đáng nhớ

- Vận dụng hằng đẳng thức để biến đổi đa thức thành tích các nhân tử hoặc lũy thừa của một đa thức đơn giản.

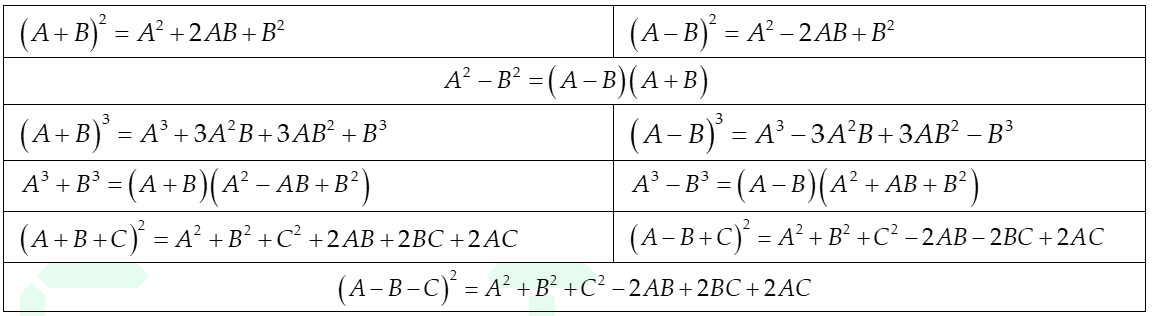
Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

B. Cách phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử

a) Đối với đa thức bậc hai f(x) = ax2 + bx + c có nghiệm

Phương pháp chung

Bước 1: Tìm tích ac rồi phân tích ac ra tích của hai thừa số nguyên bằng mọi cách

Bước 2: Chọn hai thừa số trong các tích trên có tổng bằng b

Bước 3: Tách bx = aix + cix. Từ đó nhóm hai số hạng thích hợp để phân tích tiếp

Ví dụ: Phân tích đa thức f(x) = 3x2 + 8x + 4 thành nhân tử

Hướng dẫn giải

Phân tích ac:

ac = 12 = 3.4 = (-3).(-4) = 2.6 = (-2). (-6) = 1.12 = (-1).(-12)

Tích của hai thừa số có tổng bằng b = 8 là tích ac = 2.6

Tách 8x = 2x + 6x

=> 3x2 + 8x + 4 = 3x2 + 2x + 6x + 4 = (3x2 + 2x) + (6x + 4)

= x(3x + 2) + 2(3x + 2) = (x + 2)(3x + 2)

b) Đối với đa thức hai biến dạng f(x; y) = ax2 + bxy + cy2

Phương pháp chung

Phương pháp 1: Xem đa thức f(x; y) = ax2 + bxy + cy2 là đa thức một biến x

Khi đó hệ số lần lượt là a, by, xy2 và ta áp dụng phương pháp như với đa thức bậc hai một biến.

Phương pháp 2: Viết đa thức về dạng f\left( {x;y} \right) = {y^2}\left[ {a{{\left( {\frac{x}{y}} \right)}^2} + b{{\left( {\frac{x}{y}} \right)}^2}} \right]. Đặt t = \frac{x}{y} và phân tích đa thức at2 + bt + c theo phương pháp như với đa thức bậc hai một biến.

Ví dụ: Phân tích đa thức 2x2 – 5xy + 2y2 thành nhân tử

Hướng dẫn giải

Cách 1: Xét đa thức f(x) = 2x2 – 5xy + 2y2

Khi đó ta có a = 2; b = -5y; c = 2y2

Ta có ac = y.4y = (-y).(-4y) = 2y.2y = (-2y).(-2y) = ….

Ta chọn tích (-y).(-4y) vì (-y) + (-4y) = -5y = b

=> 2x2 – 5xy + 2y2 = 2x2 – xy – 4xy + 2y2 = x(2x – y) – 2y(2x – y) = (x – 2y)(2x – y)

Cách 2: Xét đa thức f\left( {x;y} \right) = {y^2}\left( {\frac{{2.{x^2}}}{{{y^2}}} - 5\frac{x}{y} + 2} \right)

Đặt \[t = \frac{x}{y}\] và ta có đa thức 2t2 – 5t + 2 = 2t2 – t – 4t + 2 = (2t – 1)(t – 2)

Khi đó ta được f(x; y) = y2(2t – 1)(t – 2) = {y^2}.\left( {2\frac{x}{y} - 1} \right)\left( {\frac{x}{y} - 2} \right) = (2x – y)(x – 2y)

Chú ý: Quy tắc dấu ngoặc

Khi bỏ dấu ngoặc có dấu "−" đứng trước, ta phải đối dấu tất cả các số hạng trong dấu ngoặc: dấu "−“ thành dấu "+" và dấu "+” thành dấu "−". Khi bỏ dấu ngoặc có dấu "+" đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên.

C. Bài tập phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử

Ví dụ: Dùng hằng đẳng thức phân tích đa thức thành nhân tử:

a. {\left( {x - 3} \right)^2} - {\left( {2 - 3x} \right)^2}

b. {\left( {x + 1} \right)^3} + {\left( {x - 2} \right)^3}

c. {x^2} + 2xy + {y^2} - 4

Hướng dẫn giải

a. Ta có:

\begin{matrix} {\left( {x - 3} \right)^2} - {\left( {2 - 3x} \right)^2} \hfill \\ = \left( {x - 3 + 2 - 3x} \right)\left( {x - 3 - 2 + 3x} \right) \hfill \\ = \left( { - 2x - 1} \right)\left( {4x - 5} \right) \hfill \\ \end{matrix}

b. Ta có:

\begin{matrix} {\left( {x + 1} \right)^3} + {\left( {x - 2} \right)^3} \hfill \\ = \left( {x + 1 + x - 2} \right)\left[ {{{\left( {x + 1} \right)}^2} - \left( {x + 1} \right)\left( {x - 2} \right) + {{\left( {x - 2} \right)}^2}} \right] \hfill \\ = \left( {2x - 1} \right)\left[ {{x^2} + 2x + 1 - \left( {{x^2} - 2x + x - 2} \right) + {x^2} - 4x + 4} \right] \hfill \\ = \left( {2x - 1} \right)\left[ {{x^2} + 2x + 1 - {x^2} + x + 2 + {x^2} - 4x + 4} \right] \hfill \\ = \left( {2x - 1} \right)\left( {{x^2} - x + 7} \right) \hfill \\ \end{matrix}

c. Ta có:

\begin{matrix} {x^2} + 2xy + {y^2} - 4 \hfill \\ = \left( {{x^2} + 2xy + {y^2}} \right) - {2^2} \hfill \\ = {\left( {x + y} \right)^2} - {2^2} \hfill \\ = \left( {x + y - 2} \right)\left( {x + y + 2} \right) \hfill \\ \end{matrix}

D. Bài tập phân tích đa thức thành nhân tử

Bài tập 1: Phân tích đa thức thành nhân tử:

a. {x^2} - 9

b. 4{x^2} - 25

c. {x^6} - {y^6}

d. 9{x^2} + 6xy + {y^2}

e. 6x - 9 - {x^2}

f. {x^2} + 4{y^2} + 4xy

g. 25{a^2} + 10a + 1

h. {\left( {x + y} \right)^2} - {\left( {x - y} \right)^2}

i. 10ab + 0,25{a^2} + 100{b^2}

k. {\left( {3x + 1} \right)^2} - {\left( {x + 1} \right)^2}

Bài tập 2: Tìm x biết: (Sử dụng hằng đẳng thức)

a. {x^3} - 6{x^2} + 12x - 8 = 0

b. 16{x^2} - 9{\left( {x + 1} \right)^2} = 0

c. - 27 + {x^3} - 9{x^2} + 27x = 0

Bài tập 3: Chứng minh rằng với mọi số nguyên n ta có:

{\left( {4n + 3} \right)^2} - 25 chia hết cho 8

Bài tập 4: Dùng hằng đẳng thức phân tích đa thức sau thành nhân tử

{\left( {x - y} \right)^3} + {\left( {y - z} \right)^3} + {\left( {z - x} \right)^3}

Bài tập 5: Phân tích đa thức thành nhân tử:

a. \frac{1}{{36}}{a^2} - \frac{1}{4}{b^2}

b. {\left( {a + x} \right)^2} - 25

c. {x^2} + 2x + 1 - {y^2} + 2y - 1

d. - 125{a^3} + 75{a^2} - 15a + 1

Bài tập 6: Phân tích đa thức thành nhân tử (bằng kĩ thuật bổ sung hằng đẳng thức)

a. {x^2} - 3xy - 2{y^2}

b. {x^2} - x - xy - x{y^2} + 2y

c. {x^2} - xy + x - 2{y^2} + y

d. {x^2} + 4xy + 2x + 3{y^2} + 6y

-------------------------------------------------

GiaiToan.com đã gửi tới các bạn tài liệu Chuyên đề phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức. Ngoài ra, các em học sinh có thể tham khảo thêm các tài liệu khác như Giải Toán 8, Giải Bài tập Toán 8, Luyện tập Toán 8, để học tốt môn Toán hơn và chuẩn bị cho các bài thi đạt kết quả cao. Chúc các em học tập tốt!

  • 17.571 lượt xem
Chia sẻ bởi: Bơ
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Lý thuyết Toán 8