Hàm số là gì? Đồ thị hàm số

2 Đánh giá

Chuyên đề Toán: Hàm số

1) Hàm số
2) Hàm số bậc nhất
- Cách vẽ đồ thị hàm số bậc nhất
3) Hàm số bậc hai
- Cách vẽ đồ thị hàm số bậc hai

GiaiToan.com biên soạn và đăng tải tài liệu Hàm số giúp học sinh hiểu rõ về định nghĩa hàm số, hàm số bậc nhất, hàm số bậc hai, hàm số đồng biến nghịch biến khi nào?, tìm tập xác định của hàm số, .... kèm theo đó là bài tập rèn luyện có hướng dẫn chi tiết mời các em học sinh cùng tham khảo. Chúc các bạn học tập tốt!

1) Hàm số

- Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao với mỗi giá trị của x ta luôn xác định chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và gọi x là biến số.

2) Hàm số bậc nhất

- Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là những số cho trước và a ≠ 0.

Ví dụ: y = -2x; y = x – 3; y = 5 – 3x, ….

- Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc $\mathbb{R}$ và có tính chất sau:

a) Hàm số đồng biến trên $\mathbb{R}$ khi a > 0

b) Hàm số nghịch biến trên $\mathbb{R}$ khi a < 0

Ví dụ:

Hàm số y = -2x có a = -2

=> Hàm số y = -2x là hàm số nghịch biến trên $\mathbb{R}$

Hàm số y = x – 3 có a = 1

=> Hàm số y = x – 3 là hàm số đồng biến trên $\mathbb{R}$

Cách vẽ đồ thị hàm số bậc nhất

- Vì đồ thị hàm số bậc nhất là một đường thẳng nên muốn vẽ ta chỉ cần xác định hai điểm phân biệt bất kỳ trên đường thẳng đó.

3) Hàm số bậc hai

- Hàm số bậc hai là hàm số có công thức $y = a{x^2} + bx + c;\left( {a \ne 0} \right)$ và có miền xác định $D = \mathbb{R}$

- Đồ thị của hàm số bậc hai chính là bậc parabol với đỉnh là điểm $I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$ có trục đối xứng là đường thẳng $x = - \frac{b}{{2a}}$

- Parabol có bề lõm quay lên trên nếu như a > 0 và quay xuống nếu như a < 0

Với a > 0 thì

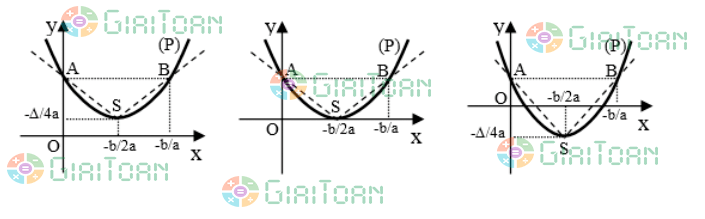
Hàm số là gì?

Với a < 0 thì

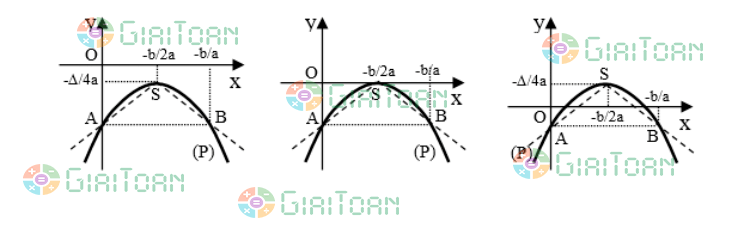
Hàm số là gì?

Cách vẽ đồ thị hàm số bậc hai

Để vẽ đường parabol y = ax² + bx + c; (a ≠ 0), ta thực hiện các bước sau:

Xác định tọa độ đỉnh là điểm $I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$
Vẽ trục đối xứng d là đường thẳng $x = - \frac{b}{{2a}}$
Xác định giao điểm của parabol với các trục tọa độ (nếu có). Xác định thêm một số điểm thuộc đồ thị. Chẳng hạn, điểm đối xứng với giao điểm của đồ thị với trục tung qua trục đối xứng của parabol.
Vẽ parabol, dựa vào kết quả trên, chú ý bề lõm của đồ thị khi a > 0, a < 0.

---------------------------------------------

Hy vọng tài liệu mà GiaiToan.com giới thiệu sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết, cách giải bài tập từ đó vận dụng giải các bài toán chuyên đề Hàm số một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học. Chúc các em học tốt.

Chia sẻ bởi: