Giaitoan.com Toán 8 Lý thuyết Toán 8

Toán 8 Bài 3 Hình thang cân Tứ giác

Nội dung
  • 1 Đánh giá

Hình thang cân

GiaiToan.com xin giới thiệu đến quý thầy cô và học sinh Toán lớp 8 Bài 3 Hình thang cân SGK Toán 8 tập 1 dưới sự trình bày chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 8 giúp cho các bạn học sinh ôn tập và củng cố lý thuyết môn Toán lớp 8 vững vàng. Mời các bạn tham khảo!

I. Hình thang cân là gì

- Hình thang cân là hình thang có hai góc kề một đáy bằng nhau

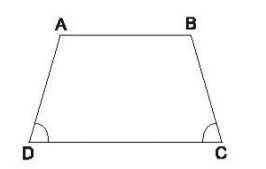
Xét hình thang cân ABCD có  \Leftrightarrow \left\{ \begin{array}{l} AB//CD\\ \widehat C = \widehat D;\,\widehat B = \widehat A \end{array} \right.

II. Tính chất của hình thang

- Trong hình thang cân, hai cạnh bên bằng nhau

- Trong hình thang cân, hai đường chéo bằng nhau

III. Dấu hiệu nhận biết

- Hình thang có hai đường chéo bằng nhau

- Hình thang có hai góc kề một đáy bằng nhau

Ví dụ 1: Cho tam giác MKN cân tại M có đường phân giác MH. Gọi I là một điểm nàm giữa M và H. Tia KI cắt MN tại A, tia NI cắt MK tại B

a) Chứng minh ABKN là hình thang cân

b) Chứng minh MI là đường trung trực của AB và KN

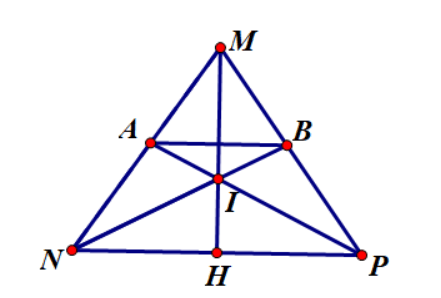
Hướng dẫn giải

a) Xét tam giác MKN cân tại M có:

MH là phân giác\Rightarrow MH là đường trung trực của NK

Mà  I \in MH \Rightarrow IN = IK ( tính chất điểm nằm trên đường trung trực của đoạn thẳng)

\Rightarrow \Delta INK cân tại I

\Rightarrow \widehat {INK} = \widehat {IKN} = \dfrac{{{{180}^ \circ } - \widehat {NIK}}}{2}

Xét \Delta ANK và  \Delta BKNcó

\begin{array}{l} \widehat {ANK} = \widehat {BKN}\\ \widehat {AKN} = \widehat {BN}K \end{array}

NK là cạnh chung

\Delta ANK = \Delta BKN\left( {g.c.g} \right)

\Rightarrow AK = BN( hai cạnh tương ứng)

Mà  IK = IN\left( {cmt} \right)

\Rightarrow AK - IK = BN - IN hay AI = BI \Rightarrow \Delta IAB  cân tại I

\Rightarrow \widehat {IAB} = \widehat {IBA} = \dfrac{{{{180}^ \circ } - \widehat {AIB}}}{2}

Mà \widehat {AIB} = \widehat {NI}K ( hai góc đối đỉnh)

\Rightarrow \widehat {INK} = \widehat {IBA} mà hai góc ở vị trí so le trong \Rightarrow AB//NK (đpcm)

b) Có ABKN là hình thang cân \Rightarrow AN = BK

Mà MN = MK\Rightarrow MN - AN = MK - BK hay MA = MB

\Rightarrow M \in  đường trung trực của AB

Mà AI = BI \Rightarrow I \in đường trung trực của AB

\Rightarrow MI là đường trung trực của AB

Mà MI là đường trung trực của KN

\Rightarrow MI vừa là đường trung trực của AB vừa là đường trung trực của KN

Bài tiếp theo: Toán 8 Bài 4 Đường trung bình của tam giác, hình thang

Bài liên quan:

---------------------------------------------

Trên đây là Lý thuyết Tứ giác dành cho các em học sinh tham khảo, nắm chắc được lí thuyết Toán lớp 8 Chương 1: Tứ giác. Qua đó giúp các em học sinh ôn tập nắm chắc kiến thức cơ bản môn Toán 8 và hỗ trợ các em học sinh trong các kì thi trong năm học lớp 8. Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu tham khảo: Luyện tập Toán 8, Giải Toán 8 tập 1, Lí thuyết Toán 8, ...

  • 23 lượt xem
Chia sẻ bởi: Lê Thị Thùy
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Lý thuyết Toán 8