Đường trung bình của tam giác Bài tập Toán 8
Bài tập Đương trung bình của tam giác
Đường trung bình của tam giác lớp 8 được GiaiToan.com biên soạn bao gồm bài tập và đáp án chi tiết giúp các bạn học sinh có thể luyện tập thêm các dạng bài tập cơ bản và nâng cao để biết được cách giải các bài toán đường trung bình. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán 8.
A. Đường trung bình của tam giác
Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm hai cạnh của tam giác đó.
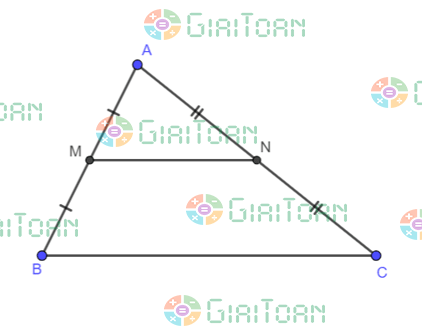
Ví dụ: Cho tam giác ABC, lấy M là trung điểm của AB, N là trung điểm của AC.

Khi đó đoạn thẳng MN là đường trung bình của tam giác ABC.
B. Tính chất đường trung bình của tam giác
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.
Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trong điểm một cạnh và song song với cạnh thứ hai thì nó đi qua trong điểm của cạnh thứ ba.
Cho tam giác ABC, M và N lần lượt là trung điểm của AN và AC.
| Kết luận: MN // BC
|
C. Bài tập đường trung bình của tam giác
Ví dụ 1: Cho tam giác ABC có các trung tuyến BD và CE. Trên cạnh BC lấy điểm M và N sao cho BM = MN = NC. Gọi I là giao điểm của AM và BD, K là giao điểm của AN và CE. Chứng minh rằng:
a) BCDE là hình thang
b) K là trung điểm của EC
c) BC = 4IK
Hướng dẫn giải
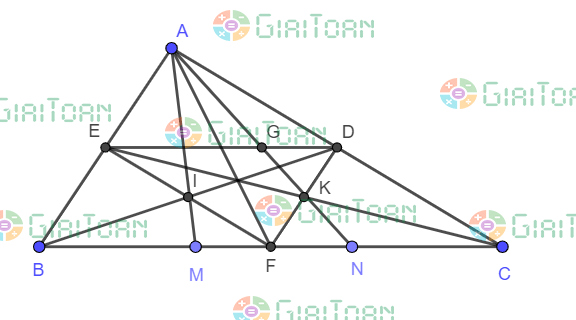
a) Xét tam giác ABC có E, D lần lượt là trung điểm của AB và AC
⇒ DE là đường trung bình của tam giác ABC
⇒ DE // BC hay BCDE là hình thang
b) Gọi G là giao điểm của AN và DE.
Ta có: E là trung điểm của AB và ED // BN
⇒ G là trung điểm của AN
⇒ EG là đường trung bình của tam giác ANB
⇒ ![]()
Ta lại có: ![]()
⇒ G là trọng tâm tam giác ACE
⇒ AK là trung tuyến của tam giác ACE
![]() ⇒ K là trung điểm của EC
⇒ K là trung điểm của EC
c) Chứng minh tương tự ta có I là trung điểm của EF.
Gọi F là trung điểm của BC, ta có: DF // AB và DK // AB
⇒ D, K, F thẳng hàng
⇒ K là trung điểm của DF.
⇒ IK là đường trung bình của tam giác DEF hay ![]()
Mà ![]() ⇒ BC = 4IK
⇒ BC = 4IK
D. Bài tập tự luyện
Bài tập 1: Tìm số đo x trong các hình sau:

Bài tập 2: Cho tam giác ABC có trung tuyến AM. Trên AC lấy điểm E, F sao cho AE = EF = FC, BE cắt AM tạo O
a) Chứng minh OEFM là hình thang
b) Chứng minh BO = 3OE
Bài tập 3: Cho hình thang ABCD có góc A và góc D vuông, AB = 2AD = 2CD. Kẻ CH vuông góc với AB tại H.
a) Tính số đo các góc của hình thang ABCD.
b) Chứng minh rằng tam giác ABC vuông cân
c) Tính chu vi hình thang nếu AB = 6cm.
d) Gọi O là giao điểm của AC và DH, O’ là giao điểm của BD và CH. Chứng minh rằng AB = 4OO’.
Bài tập 4: Cho tam giác đều ABC. Trên tia đối của tia AB lấy điểm D và trên tia đối của tia AC ta lấy điểm E sao cho AD = AE. Gọi M, N, P, Q theo thứ tự là trung điểm của các đoạn thẳng BE, AD, AC, AB.
a) Chứng minh tứ giác BCDE là hình thang cân.
b) Chứng minh rằng tứ giác CNEQ là hình thang.
c) Trên tia đối của tia MN lấy N’ sao cho N’M = MN. Chứng minh rằng BN’ vuông góc với BD, EB = 2MN.
d) Tam giác MNP là tam giác đều.
Bài tập 5: Cho hình thang ABCD. Lấy M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.
a) Chứng minh MN // AC
b) Tứ giác MNPQ là hình gì?
-------------------------------------------------------------