Bài 6 trang 92 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

1 Đánh giá

Bài 6 trang 92 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan biên soạn và đăng tải. Hướng dẫn các em trả lời câu hỏi trong bài Toán lớp 10 bài 5: Tích của một số với một vectơ, giúp các em ôn tập, rèn luyện kỹ năng giải bài Toán. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

Bài 6 trang 92 Toán 10 Tập 1

Đề bài

Cho ABCD là hình bình hành. Đặt $\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b$ . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto $\overrightarrow {AG} ,\overrightarrow {CG}$ theo hai vecto $\overrightarrow a ,\overrightarrow b$ .

Phương pháp giải

Quy tắc cộng: $\overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD}$ với B, A, D bất kì.

Bước 1: Biểu diễn vecto $\overrightarrow {BD}$ theo hai vecto $\overrightarrow a ,\overrightarrow b$ .

Bước 2: Biểu diễn vecto $\overrightarrow {BG}$ theo hai vecto $\overrightarrow a ,\overrightarrow b$ dựa vào đẳng thức $\overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD}$

Bước 3: Biểu thị các vecto $\overrightarrow {AG} ,\overrightarrow {CG}$ theo vecto $\overrightarrow {BG}$ và $\overrightarrow a ,\overrightarrow b$ .

Lời giải chi tiết

Cách 1:

Gọi O là giao điểm của AC và BD.

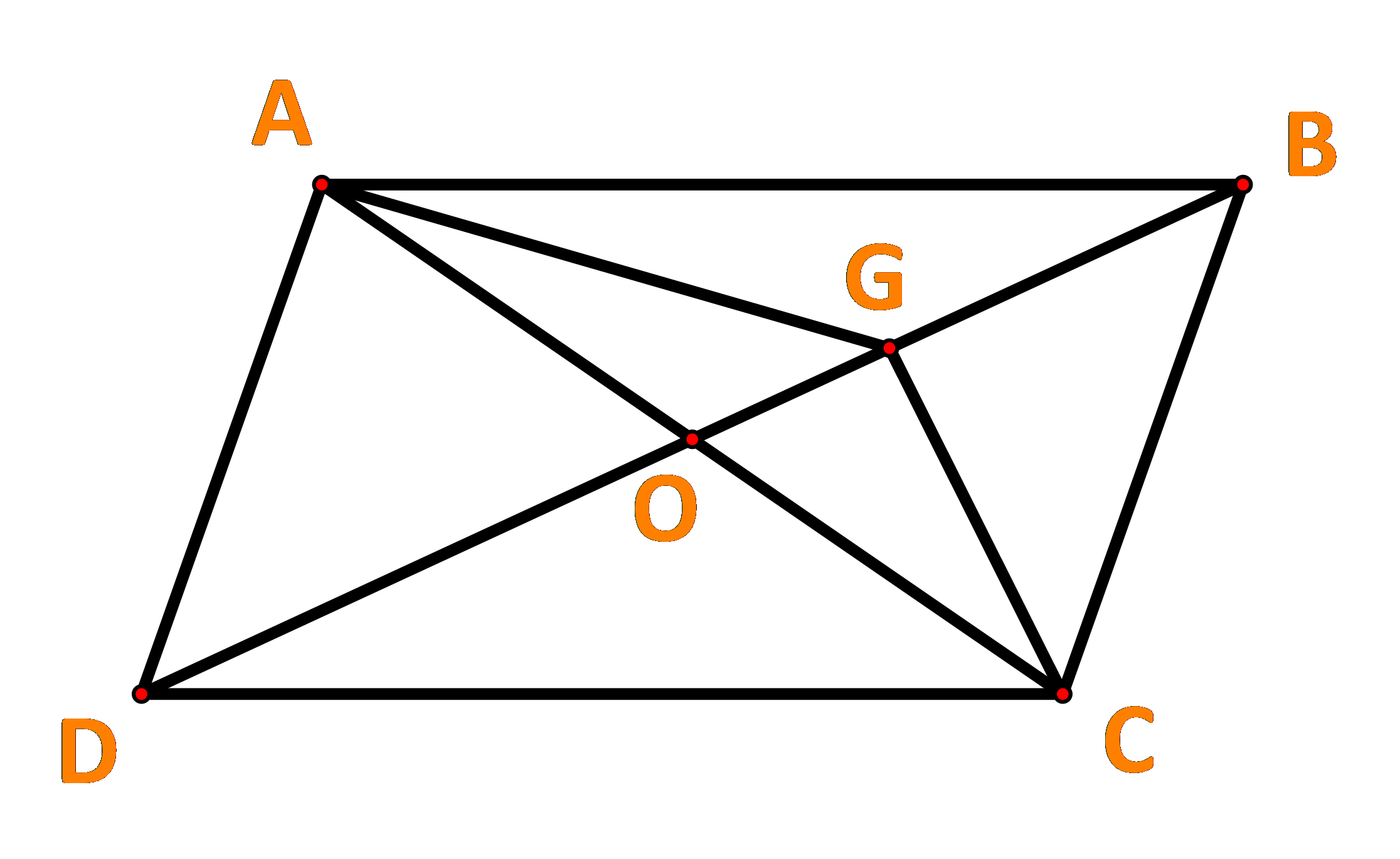
Bài 6 trang 92 Toán 10 Tập 1

Ta có:

$\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}(*)$

Lại có: $\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b$ .

$\overrightarrow {BG} ,\overrightarrow {BD}$ cùng phương và $\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|$

$\Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)$

Do đó $(*) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.$

Vậy $\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .$

Cách 2:

Gọi AE, CF là các trung tuyến trong tam giác ABC.

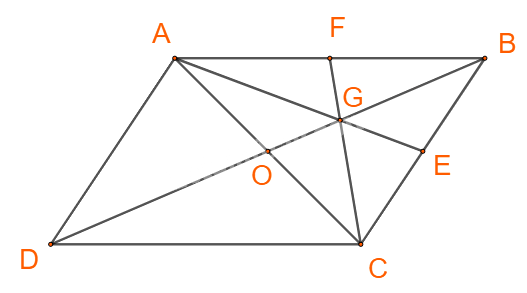
Bài 6 trang 92 Toán 10 Tập 1

Ta có:

$\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right]$

$= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b$

$\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right]$

$= \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b$

Vậy $\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .$

>>> Câu hỏi cùng bài:

>>> Bài tập tiếp theo: Giải Toán 10 Bài 6 chương 4: Tích vô hướng của hai vectơ sách Cánh Diều

Bài 6 trang 92 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan chia sẻ trên đây. Với phần hướng dẫn câu hỏi chi tiết này sẽ là tài liệu hữu ích cho các em tham khảo, qua đó nắm được cách giải các dạng bài toán lớp 10 bài 5: Tích của một số với một vectơ. Từ đó chuẩn bị tốt cho các bài thi giữa học kì và cuối kì môn Toán lớp 10. Ngoài việc tham khảo bài 6 trang 92, các em có thể tham khảo thêm các dạng bài Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều tập 1 do GiaiToan biên soạn và đăng tải nhé.

Chia sẻ bởi: