Bài 5 trang 30 Toán 10 tập 1 SGK Cánh Diều Giải Toán 10

4 Đánh giá

Bài 5 SGK Toán 10 trang 30

Toán 10 trang 30 Bài 5 là lời giải Bài tập cuối chương II SGK Toán 10 Cánh Diều được GiaiToan.com biên soạn. Lời giải Toán 10 này với hướng dẫn chi tiết lời giải giúp cho các bạn học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán. Mời các bạn học sinh cùng tham khảo chi tiết.

Giải Bài 5 Toán 10 trang 30

Đề bài: Một chuỗi nhà hàng ăn nhanh bán đồ ăn từ 10h00 dáng đến 22h00 mỗi ngày. Nhân viên phục vụ của nhà hàng làm việc theo hai ca, mỗi ca 8 tiếng, ca I từ 10h00 đến 18h00 và ca II từ 14h00 đến 22h00.

Tiền lương của nhân viên được tính theo giờ (bảng bên).

Khoảng thời gian làm việc	Tiền lương/ giờ
10h00 – 18h00	20 000 đồng
14h00 – 22h00	22 000 đồng

Để mỗi nhà hàng hoạt động được thì cần tối thiểu 6 nhân viên trong khoảng 10h00 – 18h00, tối thiểu 24 nhân viên trong thời gian cao điểm 14h00 – 18h00 và không quá 20 nhân viên trong khoảng 18h00 – 22h00. Do lượng khách trong khoảng 14h00 – 22h00 thường đông hơn nên nhà hàng cần số nhân viên ca II ít nhất phải gấp đôi số nhân viên ca I. Em hãy giúp chủ chuỗi nhà hàng chỉ ra cách huy động số lượng nhân viên cho mỗi ca sao cho chi phí tiền lương mỗi ngày là ít nhất.

Hướng dẫn:

Đọc kỹ đề bài để tìm ra hệ bất phương trình bậc nhất hai ẩn thích hợp. Sử dụng hệ bất phương trình bậc nhất hai ẩn để giải bài toán.

Lời giải:

Gọi $x,y$ lần lượt là số nhân viên của ca I và II trong một ngày làm việc ( $x,y \in \mathbb{N}$ )

Theo đề bài, cần tối thiểu 6 nhân viên trong khoảng từ 10h00 – 18h00, ta có bất phương trình: $x \geqslant 6$ .

Cần tối thiểu 24 nhân viên trong thời gian cao điểm 14h00 – 18h00, ta có bất phương trình: $x + y \geqslant 24$

Không quá 20 nhân viên trong khoảng 18h00 – 22h00, ta có bất phương trình: $y \leqslant 20$ .

Trong khoảng 14h00 – 22h00, nhà hàng cần số nhân viên ca II ít nhất phải gấp đôi số nhân viên ca I, ta có bất phương trình: $2x \leqslant y$ .

Tổng số tiền lương của các nhân viên ca I là: $160000x$ (đồng)

Tổng số tiền lương của các nhân viên ca II là: $176000y$ (đồng)

Chi phí tiền lương mỗi ngày của nhà hàng là: $T = 160000x + 176000y$

Bài toán đưa về: Tìm $x,y$ là nghiệm của hệ bất phương trình:

$\left\{ \begin{gathered} x \geqslant 6 \hfill \\ x + y \geqslant 24 \hfill \\ y \leqslant 20 \hfill \\ 2x \leqslant y \hfill \\ \end{gathered} \right.$ sao cho $T = 160000x + 176000y$ có giá trị nhỏ nhất.

Xác định miền nghiệm của hệ bất phương trình được:

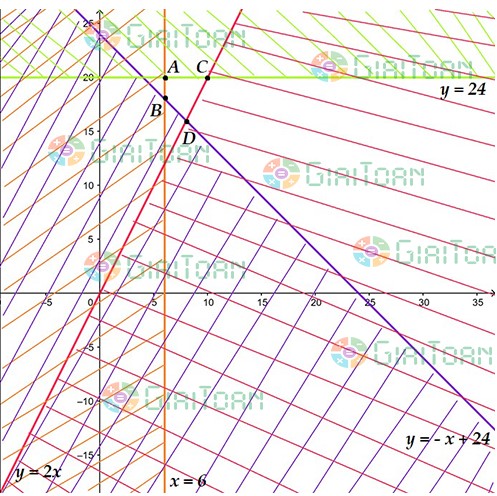
Bài 5 trang 30 Toán 10 tập 1 SGK Cánh Diều

Miền nghiệm của hệ bất phương trình là tứ giác $ABDC$ .

Biểu thức $T = 160000x + 176000y$ có giá trị nhỏ nhất tại một trong các đỉnh của tứ giác $ABDC$ .

Đỉnh $A$ là giao điểm của hai đường thẳng $y = 20$ và $x = 6$ . Tọa độ của đỉnh $A$ là $A\left( {6;20} \right)$ .

Đỉnh $B$ là giao điểm của hai đường thẳng $x = 6$ và $y = - x + 24$ . Tọa độ của đỉnh $B$ là $B\left( {6;18} \right)$ .

Đỉnh $C$ là giao điểm của hai đường thẳng $y = 24$ và $y=2x$ . Tọa độ của đỉnh $C$ là $C\left( {12;24} \right)$

Đỉnh $D$ là giao điểm của hai đường thẳng $y = - x + 24$ và $y=2x$ . Tọa độ của đỉnh $D$ là $D\left( {8;16} \right)$

Thay tọa độ điểm $A\left( {6;20} \right)$ vào T có: $T = 160000.6 + 176000.20 = 4480000$

Thay tọa độ điểm $B\left( {6;18} \right)$ vào T có: $T = 160000.6 + 176000.18 = 4128000$

Thay tọa độ điểm $C\left( {12;24} \right)$ vào T có: $T = 160000.6 + 176000.20 = 5440000$

Thay tọa độ điểm $D\left( {8;16} \right)$ vào T có: $T = 160000.8 + 176000.16 = 4096000$

Vậy biểu thức $T = 160000x + 176000y$ có giá trị nhỏ nhất tại điểm $D\left( {8;16} \right)$ với $x = 8;\,\,y = 16$ .

Vậy để huy động số lượng nhân viên cho mỗi ca sao cho chi phí tiền lương mỗi ngày là ít nhất thì ca I cần 8 nhân viên và ca II cần 16 nhân viên.

-----> Bài tiếp theo: Hoạt động 1 trang 31 Toán 10 tập 1 SGK Cánh Diều

----------------

Trên đây là lời giải chi tiết Toán 10 trang 30 Bài 5 cho các bạn học sinh tham khảo, nắm được cách giải các dạng toán của Chương II: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn. Qua đó giúp các bạn học sinh ôn tập chuẩn bị cho các bài thi giữa học kì và cuối học kì lớp 10.

Chia sẻ bởi: