Bài 8 trang 98 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

1 Đánh giá

Bài 8 trang 98 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan biên soạn và đăng tải. Hướng dẫn các em trả lời câu hỏi trong bài Toán lớp 10 bài 6: Tích vô hướng của hai vectơ, giúp các em ôn tập, rèn luyện kỹ năng giải bài tập Toán lớp 10. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

Bài 8 trang 98 Toán 10 Tập 1

Đề bài

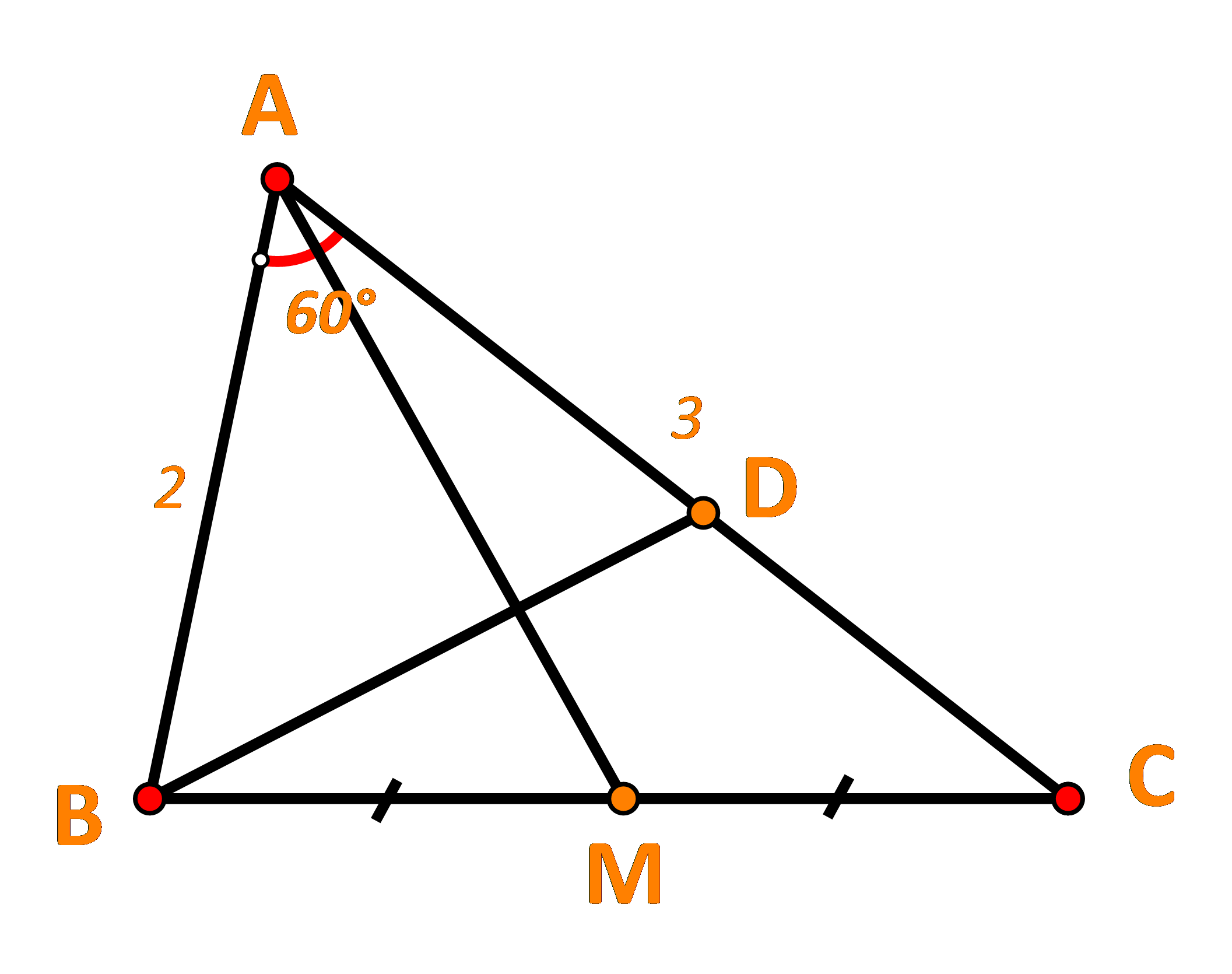
Cho tam giác ABC có AB = 2, AC = 3, $\widehat {BAC} = {60^o}$ . Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn $\overrightarrow {AD} = \frac{7}{{12}}\overrightarrow {AC}$ .

a) Tính $\overrightarrow {AB} .\overrightarrow {AC}$

b) Biểu diễn $\overrightarrow {AM} ,\overrightarrow {BD}$ theo $\overrightarrow {AB} ,\overrightarrow {AC}$

c) Chứng minh AM \bot BD.

Phương pháp giải

+) Tính $\overrightarrow {AB} .\overrightarrow {AC}$ bằng công thức $\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos (\overrightarrow {AB} ,\overrightarrow {AC} ) = AB.AC.\cos \widehat {BAC}$

+) M là trung điểm $BC \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM}$ với điểm A bất kì.

+) $AM \bot BD \Leftrightarrow \overrightarrow {AM} .\overrightarrow {BD} = 0$

Lời giải chi tiết

Bài 8 trang 98 Toán 10 Tập 1

a) $\overrightarrow {AB} .\overrightarrow {AC} = 2.3.\cos \widehat {BAC} = 6.\cos {60^o} = 3$

Ta có: $\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM}$ (do M là trung điểm của BC)

$\Leftrightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC}$

+) $\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} = \frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB}$

c) Ta có:

$\begin{array}{l}\overrightarrow {AM} .\overrightarrow {BD} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} } \right)\left( {\frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} } \right)\\ = \frac{7}{{24}}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{7}{{24}}{\overrightarrow {AC} ^2} - \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} \\ = - \frac{1}{2}A{B^2} + \frac{7}{{24}}A{C^2} - \frac{5}{{24}}\overrightarrow {AB} .\overrightarrow {AC} \\ = - \frac{1}{2}{.2^2} + \frac{7}{{24}}{.3^2} - \frac{5}{{24}}.3\\ = 0\end{array}$

$\Rightarrow AM \bot BD$

>>> Câu hỏi cùng bài:

>>> Bài tập tiếp theo: Giải Toán 10 Bài tập cuối chương 4 sách Cánh Diều

Bài 8 trang 98 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ là tài liệu hữu ích cho các em tham khảo, nắm được cách giải các dạng bài toán về Tích vô hướng của hai vectơ, đồng thời chuẩn bị tốt cho kì thi giữa học kì và cuối học kì lớp 10 môn Toán sắp tới. Chúc các em học tốt, ngoài việc tham khảo tài liệu trên, GiaiToan xin chia sẻ tới các em các dạng bài Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều tập 1 do GiaiToan biên soạn và đăng tải nhé.

Chia sẻ bởi: