Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số Lý thuyết toán 9 chương 2 đại số

1 Đánh giá

Các khái niệm về hàm số

1. Hàm số là gì?
2. Đồ thị của hàm số
3. Hàm số đồng biến, nghịch biến

Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số nằm trong Lý thuyết Toán 9 tập 1 được trình bày chi tiết, rõ ràng theo khung chương trình SGK giúp cho các bạn học sinh ôn tập và củng cố lý thuyết môn Toán lớp 9.

1. Hàm số là gì?

- Nếu đại lượng y phụ thuộc vào đại lương thay đổi x sao cho với mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x được gọi là biến số

2. Đồ thị của hàm số

Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số $y = f(x)$ .

Ví dụ:

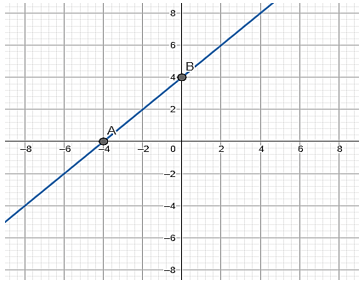
Lý thuyết Nhắc lại và bổ sung các khái niệm về hàm số

Hình bên là đồ thị của hàm số $y = f(x) = x + 4$ .

Các cặp giá trị tương ứng trên mặt phẳng tọa độ là A(-4; 0); B(0; 4).

3. Hàm số đồng biến, nghịch biến

- Cho hàm số $y = f\left( x \right)$ xác định với mọi giá trị của x thuộc $\mathbb{R}$

+ Nếu giá trị của biến x tăng lên mà giá trị tương ứng f(x) cũng tăng lên thì hàm số y= f(x) được gọi là hàm số đồng biến trên $\mathbb{R}$ ( gọi tắt là hàm số đồng biến )

+ Nếu giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi thì hàm số y=f(x) được gọi làm hàm số nghịch biến trên $\mathbb{R}$ ( gọi tắt là hàm số nghịch biến)

Nói cách khác, với ${x_1},{x_2}$ bất kì thuộc $\mathbb{R}$

+ Nếu ${x_1} < {x_2}$ mà $f{\left( x \right)_1} < f\left( {{x_2}} \right)$ thì hàm số y= f(x) đồng biến trên $\mathbb{R}$

+ Nếu ${x_1} < {x_2}$ mà $f{\left( x \right)_1} > f\left( {{x_2}} \right)$ thì hàm số y= f(x) nghịch biến trên $\mathbb{R}$

Ví dụ 1: Cho hàm số $y = f\left( x \right) = \frac{2}{3}x$ . Tính

a) $f\left( { - 4} \right)$

b) $f\left( 0 \right)$

c) $f\left( { - \dfrac{1}{2}} \right)$

Hướng dẫn giải

Ta có $y = f\left( x \right) = \dfrac{2}{3}x\,\,\,\left( * \right)$

a) Với $f\left( { - 4} \right)$ , thay x= -4 vào (*) ta được $y = f\left( { - 4} \right) = \dfrac{2}{3}\left( { - 4} \right)\, = \dfrac{{ - 8}}{3}$ .

Vậy $f\left( { - 4} \right) = \dfrac{{ - 8}}{3}$ .

b) Với $f\left( 0 \right)$ , thay x= 0 vào (*) ta được $y = f\left( 0 \right) = \dfrac{2}{3}.0\, = 0$ .

Vậy $f\left( 0 \right) = 0$ .

c) Với $f\left( { - \dfrac{1}{2}} \right)$ , thay $x = - \dfrac{1}{2}$ vào (*) ta được $y = f\left( { - \dfrac{1}{2}} \right) = \dfrac{2}{3}\left( { - \dfrac{1}{2}} \right)\, = \dfrac{{ - 1}}{3}$ .

Vậy $f\left( { - \dfrac{1}{2}} \right) = \dfrac{{ - 1}}{3}$ .

Bài tiếp theo: Toán lớp 9 Bài 2 Hàm số bậc nhất

Trên đây là Bài 1 Nhắc lại và bổ sung khái niệm về hàm số dành cho các em học sinh tham khảo, nắm chắc được lí thuyết Toán lớp 9 Chương 2: Hàm số bậc nhất. Qua đó giúp các em học sinh ôn tập nắm chắc kiến thức cơ bản môn Toán 9 và hỗ trợ các em học sinh trong các kì thi trong năm học lớp 9. Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu tham khảo: Luyện tập Toán 9, Lí thuyết Toán 9, ...