Toán 9 Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ Lý thuyết toán 9 chương 4 hình học

1 Đánh giá

Toán 9 Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ thuộc phần Lý thuyết Toán 9 tập 2 được trình bày chi tiết, rõ ràng theo khung chương trình SGK giúp cho các bạn học sinh ôn tập và củng cố lý thuyết môn Toán lớp 9.

Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ

1. Hình trụ
2. Cắt hình trụ bởi một mặt phẳng
3. Diện tích và thể tích hình trụ
4. Ví dụ cụ thể

1. Hình trụ

Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.

+ Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.

+ Đường thẳng AB được gọi là trục của hình trụ.

+ Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.

Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ

2. Cắt hình trụ bởi một mặt phẳng

+ Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.

+ Khi cắt hình trụ bởi một mặt phẳng song song với trục OO' thì mặt cắt là một hình chữ nhật

Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ

3. Diện tích và thể tích hình trụ

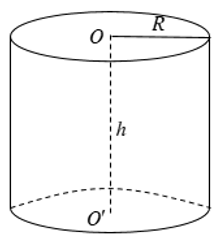
Cho hình trụ có bán kính đáy R và chiều cao h.

+ Diện tích xung quanh: $S_{xq} = πRh$

+ Diện tích toàn phần: $S_{tp} = 2πRh + 2πR^{2}$

+ Thể tích: $V = πR^{2} h$

Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ

4. Ví dụ cụ thể

Câu 1: Một hình trụ có bán kính đáy bằng 1/4 đường cao. Khi cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt là một hình chữ nhật có diện tích là 50cm². Tính diện tích xung quanh và thể tích hình trụ.

Hướng dẫn:

Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ

Theo giả thiết ta có: $r = \frac{1}{4} h$ Mà $S_{hcn} = h \times 2r = 50 cm^{2}$

Khi đó ta có: $S_{hcn} = (2 \times \frac{1}{4} h)\times h = 50 \Leftrightarrow h^{2} = 100 \Leftrightarrow h = 10$ (cm)

$\Rightarrow r = \frac{1}{4} h = \frac{5}{2}$ cm

Do đó $\left\{\begin{matrix} V = πr^{2} h = 62,5π (cm^{3}) \\ S_{xq} = 2πrh = 50π (cm^{2} ) \end{matrix}\right.$

>>>> Bài tiếp theo: Lý thuyết Hình nón, Hình nón cụt, Diện tích xung quanh và thể tích của hình nón, hình nón cụt

Trên đây là Lý thuyết Hình Trụ - Diện tích xung quanh và thể tích của hình trụ dành cho các em học sinh tham khảo, nắm chắc được lí thuyết Toán lớp 9 Chương 4: Hình trụ - Hình nón - Hình cầu. Qua đó giúp các em học sinh ôn tập nắm chắc kiến thức cơ bản môn Toán 9 và hỗ trợ các em học sinh trong các kì thi trong năm học lớp 9. Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu tham khảo: Luyện tập Toán 9, Lí thuyết Toán 9, ...