Toán 9 Bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông Lý thuyết toán 9 chương 1 hình học

1 Đánh giá

Hệ thức về cạnh và đường cao trong tam giác vuông

1. Hệ thức lượng trong tam giác
2. Các dạng toán thường gặp về Một số hệ thức về cạnh và đường cao trong tam giác vuông

Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông thuộc phần Lý thuyết Toán 9 tập 1 được trình bày chi tiết, rõ ràng theo khung chương trình SGK giúp cho các bạn học sinh ôn tập và củng cố lý thuyết môn Toán lớp 9.

1. Hệ thức lượng trong tam giác

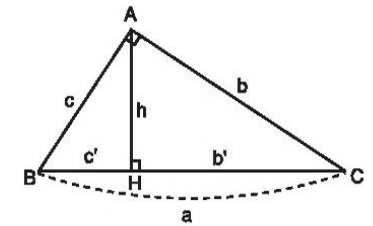
Xét tam giác ABC vuông tại A có:

- Cạnh huyền BC = a

- Các cạnh góc vuông AC = b, AB = c

- Đường cao AH = h

- Hình chiếu của AC và AB lên cạnh huyền BC lần lượt là CH = b’, BH = c’

Ta có các hệ thức lượng sau:

+ $A{B^2} = BH.BC \Rightarrow {c^2} = {c^\prime }.a$

+ $A{C^2} = CH.BC \Rightarrow {b^2} = {b^\prime }.a$

+ $A{H^2} = BH.CH \Rightarrow {h^2} = {b^\prime }.{c^\prime }$

+ $AH.BC = AB.AC \Rightarrow h.a = c.b$

+ $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Rightarrow \frac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{a^2}}}$

2. Các dạng toán thường gặp về Một số hệ thức về cạnh và đường cao trong tam giác vuông

Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông

Phương pháp:

Sử dụng hệ thức về cạnh và đường cao trong tam giác vuông.

Dạng 2: Chứng minh các hệ thức liên quan giữa các yếu tố trong tam giác vuông

Phương pháp:

Ta thường sử dụng các kiến thức:

- Đưa về hai tam giác đồng dạng có chứa các đoạn thẳng có trong hệ thức.

- Sử dụng các hệ thức về cạnh và đường cao trong tam giác vuông để chứng minh.

Ví dụ 1: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8 cm. Tính độ dài các đoạn thẳng BC, CH, BH.

Hướng dẫn giải

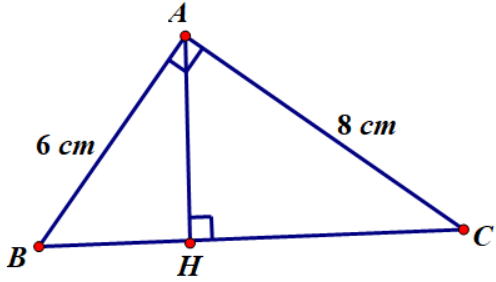
Áp dụng định lý Pytago trong tam giác ABC vuông tại A ta có:

$\begin{array}{l} A{B^2} + A{C^2} = B{C^2}\\ {6^2} + {8^2} = B{C^2}\\ \Rightarrow \,BC = 10\,\,cm \end{array}$

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A ta được

$\begin{array}{l} A{B^2} = BH.BC\\ \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}}\\ \Rightarrow BH = \dfrac{{{6^2}}}{{10}}\\ \Rightarrow BH = 3,6\,\,\left( {cm} \right) \end{array}$

$\begin{array}{l} A{C^2} = CH.BC\\ \Rightarrow CH = \dfrac{{A{C^2}}}{{BC}}\\ \Rightarrow CH = \dfrac{{{8^2}}}{{10}}\\ \Rightarrow CH = 6,4\,\,\left( {cm} \right) \end{array}$

Hoặc có thể tính BH theo cách sau:

$\begin{array}{l} CH + BH = BC\\ CH = \,BC - CH\\ CH = 10 - 3,6\\ CH = 6,4\,\left( {cm} \right) \end{array}$

Vậy BC = 10 cm, CH = 6,4 cm , BH = 3,6 cm

Bài tiếp theo: Toán 9 Bài 2 Tỉ số lượng giác của góc nhọn

Trên đây là Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông dành cho các em học sinh tham khảo, nắm chắc được lí thuyết Toán lớp 9 Chương 1: Hệ thức lượng trong tam giác vuông. Qua đó giúp các em học sinh ôn tập nắm chắc kiến thức cơ bản môn Toán 9 và hỗ trợ các em học sinh trong các kì thi trong năm học lớp 9. Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu tham khảo: Luyện tập Toán 9, Lí thuyết Toán 9, ...