Toán 10 Bài 1: Mệnh đề sách CTST Toán 10 bài 1 - Sách Chân trời sáng tạo
Lý thuyết Mệnh đề trang 7 sách Chân trời sáng tạo được GiaiToan biên soạn và đăng tải. Nội dung bài bao gồm tóm tắt lý thuyết cùng với bài tập cụ thể, giúp các em học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10. Mời các em cùng tham khảo.
Toán 10 Bài 1: Mệnh đề sách Chân trời sáng tạo
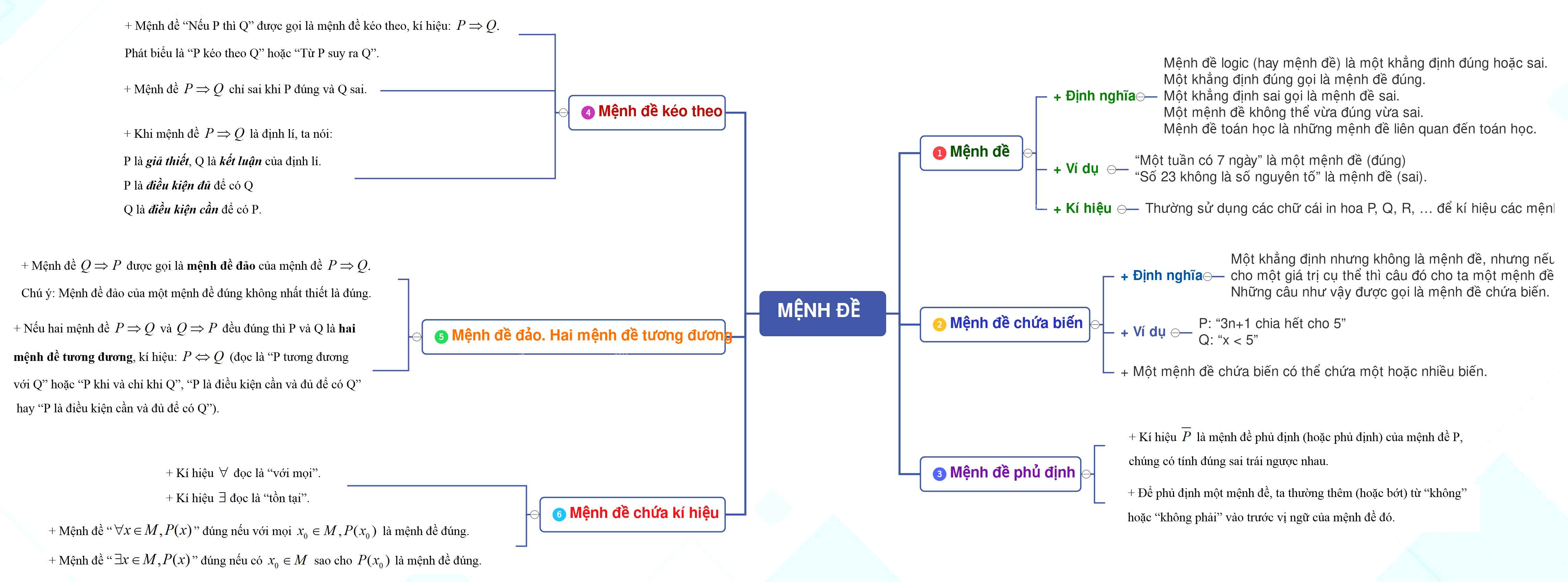
1. Mệnh đề
+ Định nghĩa:
Mệnh đề logic (hay mệnh đề) là một khẳng định đúng hoặc sai.
Một khẳng định đúng gọi là mệnh đề đúng.
Một khẳng định sai gọi là mệnh đề sai.
Một mệnh đề không thể vừa đúng vừa sai.
Mệnh đề toán học là những mệnh đề liên quan đến toán học.
+ Ví dụ:
“Một tuần có 7 ngày” là một mệnh đề (đúng)
“Số 23 không là số nguyên tố” là mệnh đề (sai).
+ Kí hiệu: Thường sử dụng các chữ cái in hoa P, Q, R, … để kí hiệu các mệnh đề.
2. Mệnh đề chứa biến
+ Một khẳng định nhưng không là mệnh đề, nhưng nếu cho một giá trị cụ thể thì câu đó cho ta một mệnh đề. Những câu như vậy được gọi là mệnh đề chứa biến.
Ví dụ: P: “3n+1 chia hết cho 5”
Q: “x < 5”
+ Một mệnh đề chứa biến có thể chứa một hoặc nhiều biến.
3. Mệnh đề phủ định
+ Kí hiệu ![]() là mệnh đề phủ định (hoặc phủ định) của mệnh đề P, chúng có tính đúng sai trái ngược nhau.
là mệnh đề phủ định (hoặc phủ định) của mệnh đề P, chúng có tính đúng sai trái ngược nhau.
+ Để phủ định một mệnh đề, ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề đó.
4. Mệnh đề kéo theo
+ Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, kí hiệu: ![]() . Phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.
. Phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.
+ Mệnh đề ![]() chỉ sai khi P đúng và Q sai.
chỉ sai khi P đúng và Q sai.
+ Khi mệnh đề ![]() là định lí, ta nói:
là định lí, ta nói:
P là giả thiết, Q là kết luận của định lí.
P là điều kiện đủ để có Q
Q là điều kiện cần để có P.
5. Mệnh đề đảo. Hai mệnh đề tương đương
+ Mệnh đề ![]() được gọi là mệnh đề đảo của mệnh đề
được gọi là mệnh đề đảo của mệnh đề ![]() .
.
Chú ý: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
+ Nếu hai mệnh đề ![]() và
và ![]() đều đúng thì P và Q là hai mệnh đề tương đương, kí hiệu:
đều đúng thì P và Q là hai mệnh đề tương đương, kí hiệu: ![]() (đọc là “P tương đương với Q” hoặc “P khi và chỉ khi Q”, “P là điều kiện cần và đủ để có Q” hay “P là điều kiện cần và đủ để có Q”).
(đọc là “P tương đương với Q” hoặc “P khi và chỉ khi Q”, “P là điều kiện cần và đủ để có Q” hay “P là điều kiện cần và đủ để có Q”).
6. Mệnh đề chứa kí hiệu 
+ Kí hiệu ![]() đọc là “với mọi”.
đọc là “với mọi”.
+ Kí hiệu ![]() đọc là “tồn tại”.
đọc là “tồn tại”.
Ví dụ:
“Mọi số thực đều có bình phương lớn hơn 2” viết là: “![]() ”
”
“Có một số thực có bình phương nhỏ hơn 2” viết là: “![]() ”
”
+ Mệnh đề “![]() ” đúng nếu với mọi
” đúng nếu với mọi ![]() là mệnh đề đúng.
là mệnh đề đúng.
+ Mệnh đề “![]() ” đúng nếu có
” đúng nếu có ![]() sao cho
sao cho ![]() là mệnh đề đúng.
là mệnh đề đúng.
7. Giải Toán 10 bài 1 SGK + SBT Chân trời sáng tạo
>>> Bài tiếp theo: Toán 10 Bài 2: Tập hợp sách CTST
Toán 10 Bài 1: Mệnh đề sách CTST được GiaiToan chia sẻ trên đây. Với phần lý thuyết cùng với bài tập này sẽ giúp các em củng cố kiến thức, cũng như áp dụng vào giải bài tập mệnh đề, từ đó chuẩn bị tốt cho bài giảng sắp tới. Chúc các em học tốt, ngoài ra các em cũng đừng quên tham khảo thêm các dạng bài tập Toán lớp 10 tại chuyên mục Giải Toán 10 CTST Tập 1 do GiaiToan biên soạn nhé.
Xem thêm bài viết khác

Thực hành 4 trang 10 Toán 10 tập 1 SGK Chân trời sáng tạo

Hoạt động 1 trang 8 Toán 10 tập 1 SGK Chân trời sáng tạo

Thực hành 3 trang 9 Toán 10 tập 1 SGK Chân trời sáng tạo

Toán 10 Bài 2: Định lí Cosin và định lí Sin sách CTST

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 độ sách CTST

Toán 10 Bài 2: Hàm số bậc hai sách CTST

Toán 10 Bài 1: Hàm số và đồ thị sách CTST

Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn sách CTST

Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách CTST

Thực hành 1 trang 7 Toán 10 tập 1 SGK Chân trời sáng tạo

Hoạt động 2 trang 8 Toán 10 tập 1 SGK Chân trời sáng tạo

Thực hành 2 trang 8 Toán 10 tập 1 SGK Chân trời sáng tạo

Hoạt động 3 trang 9 Toán 10 tập 1 SGK Chân trời sáng tạo









































