Toán 10 Bài 2: Hàm số bậc hai sách CTST Toán 10 bài 2 - Sách Chân trời sáng tạo

1 Đánh giá

Lý thuyết Hàm số bậc hai trang 49 sách Chân trời sáng tạo được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm lý thuyết cùng bài tập cụ thể giúp các em học sinh nắm vũng kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

1. Hàm số bậc hai

+ Định nghĩa:

Hàm số bậc hai biến x là hàm số cho bởi công thức dạng $y = f(x) = a{x^2} + bx + c$ với $a,b,c \in \mathbb{R};a \ne 0.$

+ Tập xác định: $\mathbb{R}$

2. Đồ thị hàm số bậc hai

+) Đồ thị hàm số bậc hai $y = f(x) = a{x^2} + bx + c (a \ne 0)$ là một parabol (P):

- Đỉnh $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$

- Trục đối xứng: đường thẳng $x = - \frac{b}{{2a}}$

- Bề lõm: quay lên trên nếu a > 0, quay xuống dưới nếu a < 0

- Cắt Oy tại điểm (0;c)

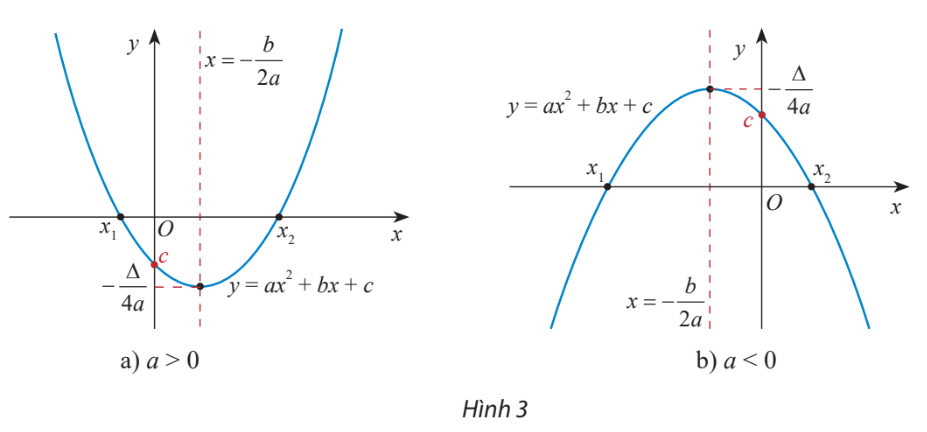
Đồ thị hàm số bậc hai

* Chú ý: Nếu PT $a{x^2} + bx + c = 0$ có hai nghiệm ${x_1},{x_2}$ thì đồ thị hàm số $y = a{x^2} + bx + c$ cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.

+) Vẽ đồ thị

1) Xác định đỉnh $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$

2) Vẽ trục đối xứng $d: x = - \frac{b}{{2a}}$

3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0;c)), trục hoành (nếu có).

Xác định $B\left( {\frac{{ - b}}{a};c} \right)$ (là điểm đối xứng với A qua d)

3. Sự biến thiên của hàm số bậc hai

+) Bảng biến thiên

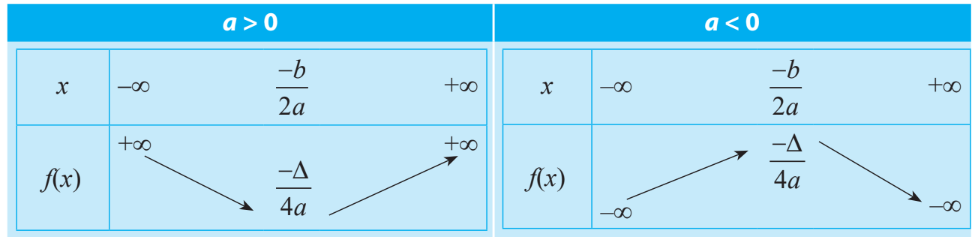
Sự biến thiên của hàm số bậc hai

+) Kết luận:

	a > 0	a < 0
Trên khoảng $\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)$	Hàm số nghịch biến	Hàm số đồng biến
Trên khoảng $\left( {\frac{{ - b}}{{2a}}; + \infty } \right)$	Hàm số đồng biến	Hàm số nghịch biến
GTLN hoặc GTNN	Đạt GTNN bằng $\frac{{ - \Delta }}{{4a}}$ tại $x = \frac{{ - b}}{{2a}}$	Đạt GTLN bằng $\frac{{ - \Delta }}{{4a}}$ tại $x = \frac{{ - b}}{{2a}}$
Tập giá trị	$T = \left[ {\left. {\frac{{ - \Delta }}{{4a}}; + \infty } \right)} \right.$	$T = \left( {\left. { - \infty ;\frac{{ - \Delta }}{{4a}}} \right]} \right.$

4. Ứng dụng của hàm số bậc hai

+) Tầm bay cao và tầm bay xa

Chọn điểm $(0;{y_0})$ là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời mặt vợt là:

$y = \frac{{ - g.{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}$

Trong đó:

g là giá tốc trọng trường $( \approx 9,8\;m/{s^2})$

$\alpha$ là góc phát cầu (so với phương ngang của mặt đất)

${v_0}$ là vận tốc ban đầu của cầu

${y_0}$ là khoảng cách từ vị trí phát cầu đến mặt đất

Quỹ đạo chuyển động của cầu lông là một parabol.

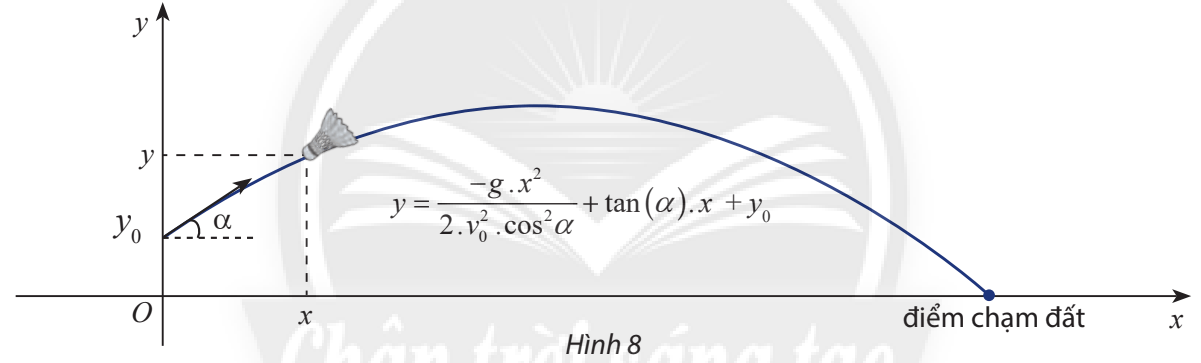
Ứng dụng của hàm số bậc hai

- Vị trí cao nhất tại đỉnh parabol, gọi là tầm bay cao;

- Khoảng cách từ nơi đứng phát cầu đến điểm cham đất, gọi là tầm bay xa.

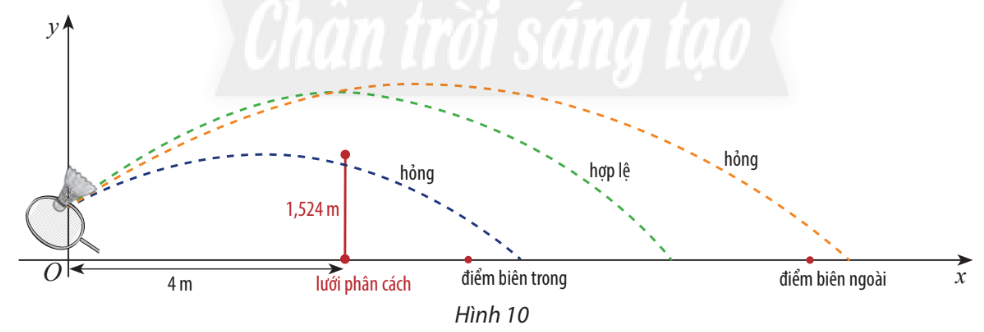
+) Bài toán ứng dụng

Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biến phía sân đối phương thì lần phát cầu được xem là hợp lệ.

Ứng dụng của hàm số bậc hai

Trắc nghiệm Toán 10 Bài 2: Hàm số bậc hai

>>> Bài tiếp theo: Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 độ sách CTST

>>> Bài trước: Toán 10 Bài 1: Hàm số và đồ thị sách CTST

Toán 10 Bài 2: Hàm số bậc hai sách CTST được GiaiToan chia sẻ trên đây. Với lý thuyết cùng bài tập cụ thể này sẽ giúp các em củng cố kiến thức, áp dụng tốt vào giải các bài tập về hàm số bậc hai, từ đó chuẩn bị tốt cho bài thi giữa học kì và cuối học kì môn Toán lớp 10 sắp tới. Chúc các em học tốt, ngoài tham khảo tài liệu trên các em cũng đừng quên tham khảo thêm các dạng bài tập Toán lớp 10 tại chuyên mục Giải Toán 10 CTST Tập 1 do GiaiToan biên soạn nhé.