Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ Toán 10 bài 2 sách Chân trời sáng tạo
Lý thuyết Toán 10 CTST bài 2
Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ chương 9 sách CTST 10 tập 2 được GiaiToan đăng tải trong bài viết dưới đây giúp các bạn dễ dàng nắm vững kiến thức trọng tâm của bài.
1. Phương trình đường thẳng
*Phương trình tham số của đường thẳng
Cho đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() . Khi đó điểm M(x: y) thuộc đường thẳng
. Khi đó điểm M(x: y) thuộc đường thẳng ![]() khi và chỉ khi tồn tại số thực t sao cho
khi và chỉ khi tồn tại số thực t sao cho ![]() , hay
, hay
![]() (2)
(2)
Hệ (2) được gọi là phương trình tham số của đường thẳng ![]() (t là tham số).
(t là tham số).
Ví dụ: Lập phương trình tham số của đường thẳng ![]() đi qua điểm A(2; -3) và có vectơ chỉ phương
đi qua điểm A(2; -3) và có vectơ chỉ phương ![]() .
.
Giải
Phương trinh tham số của đường thẳng ![]() là
là ![]()
*Phương trình tổng quát của đường thẳng
Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax + by + c =0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax + by + c =0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận ![]() là một vectơ pháp tuyến.
là một vectơ pháp tuyến.
Ví dụ: Trong mặt phẳng toạ độ, lập phương trình tổng quát của đường thẳng ![]() đi qua điểm A(2: 1) và nhận
đi qua điểm A(2: 1) và nhận ![]() là một vectơ pháp tuyến.
là một vectơ pháp tuyến.
Giải
Đường thẳng ![]() có phương trình là 3(x - 2)+ 4(y - 1) = 0 hay 3x + 4y - 10 = 0
có phương trình là 3(x - 2)+ 4(y - 1) = 0 hay 3x + 4y - 10 = 0
Nhận xét: Trong mặt phẳng toạ độ, cho đường thẳng ![]() : ax + by + c = 0
: ax + by + c = 0
+ Nếu b = 0 thì phương trình ![]() có thể đưa về dạng x = m (với
có thể đưa về dạng x = m (với ![]() ) và
) và ![]() vuông góc với Ox.
vuông góc với Ox.
+ Nếu ![]() thì phương trình
thì phương trình ![]() có thể đưa về dạng y = nx + p (với
có thể đưa về dạng y = nx + p (với ![]() )
)
* Liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng
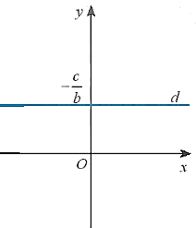
+ Nếu a=0 và ![]() thì phương trình tổng quát ax + by + c =0 trở thành y
thì phương trình tổng quát ax + by + c =0 trở thành y
Khi đó d là đường thẳng vuông góc với Oy tại điểm ![]() (Hình sau).
(Hình sau).
+ Nếu b =0 và ![]() thì phương trình tổng quát ax + by + c =0 trở thành
thì phương trình tổng quát ax + by + c =0 trở thành ![]()
Khí đó d là đường thẳng vuông góc với Ox tại điểm ![]() (Hình sau)
(Hình sau)
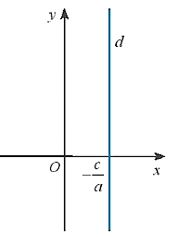
Trong cả hai trường hợp này, đường thẳng d không phải là đồ thị của hàm số bậc nhất.
2. Vị trí tương đối của hai đường thẳng
Cho ![]() và
và ![]() .
.
Toạ độ giao điểm của ![]() và
và ![]() là nghiệm của hệ phương trình:
là nghiệm của hệ phương trình:
![]() (*)
(*)
![]() cắt
cắt ![]() tại
tại ![]() ⇔ hệ (*) có nghiệm duy nhất
⇔ hệ (*) có nghiệm duy nhất ![]() .
.
![]() song song với
song song với ![]() ⇔ hệ (*) vô nghiệm.
⇔ hệ (*) vô nghiệm.
![]() trùng
trùng ![]() ⇔ hệ (*) có vô số nghiệm.
⇔ hệ (*) có vô số nghiệm.
Chú ý

Dựa vào các vectơ chỉ phương ![]() hoặc các vectơ pháp tuyến
hoặc các vectơ pháp tuyến ![]() ta có:
ta có:
+ ![]() song song hoặc trùng nhau ⇔
song song hoặc trùng nhau ⇔ ![]() cùng phương ⇔
cùng phương ⇔ ![]() cùng phương.
cùng phương.
+ ![]() cắt nhau ⇔
cắt nhau ⇔ ![]() không cùng phương ⇔
không cùng phương ⇔ ![]() không cùng phương.
không cùng phương.
Ví dụ: Xét vị trí tương đối giữa đường thẳng ![]() và mỗi đường thẳng sau:
và mỗi đường thẳng sau:

Giải
Vì 
Vậy ![]() là một, tức là chúng trùng nhau.
là một, tức là chúng trùng nhau.
Hai đường thẳng ![]() có hai vectơ pháp tuyến
có hai vectơ pháp tuyến ![]() cùng phương.
cùng phương.
Do đó, chúng song song hoặc trùng nhau. Mặt khác, điểm O(0; 0) thuộc đường thẳng ![]() nhưng không thuộc đường thẳng
nhưng không thuộc đường thẳng ![]() nên hai đường thẳng này không trùng nhau.
nên hai đường thẳng này không trùng nhau.
Vậy ![]() song song với nhau.
song song với nhau.
3. Góc giữa hai đường thẳng
- Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là số đo góc (hay đơn giản là góc) giữa hai đường thẳng.
- Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0°.
- Cho hai đường thẳng
![]() và
và ![]() .
.
Với các vectơ pháp tuyến ![]() trong ứng. Khi đó, góc
trong ứng. Khi đó, góc ![]() giữa hai đường thằng đó được xác định thông qua công thức
giữa hai đường thằng đó được xác định thông qua công thức

Ví dụ: Tính góc giữa hai đường thẳng
![]()
Giải
Vectơ pháp tuyến của ![]() là
là ![]() , của
, của ![]() là
là ![]() .
.
Gọi \varphi là góc giữa hai đường thẳng ![]() và
và ![]() . Ta có
. Ta có

Do đó, góc giữa ![]() và
và ![]() là
là ![]() .
.
4. Khoảng cách từ một điểm đến một đường thẳng
Cho điểm ![]() và đường thẳng
và đường thẳng ![]() . Khoảng cách từ điểm M đến đường thẳng
. Khoảng cách từ điểm M đến đường thẳng ![]() , kí hiệu là
, kí hiệu là ![]() , được tính bởi công thức
, được tính bởi công thức
![]()
Ví dụ: Tính khoảng cách từ điểm M(2; 4) đến đường thẳng ![]() :3x + 4y - 12 = 0.
:3x + 4y - 12 = 0.
Giải
Áp dụng công thức tính khoảng cách từ điểm M đến đường thẳng ![]() , ta có
, ta có

Vậy khoảng cách từ điểm M đến đường thẳng ![]() là 2.
là 2.
- Toán 10 Chương 9 Bài 3: Đường tròn trong mặt phẳng tọa độ
- Trắc nghiệm Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ
Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ chương 9 sách Chân trời sáng tạo do GiaiToan tổng hợp và đăng tải nhằm giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tham khảo thêm các bài lý thuyết khác được đăng tải chi tiết bám sát chương trình học SGK Chân trời sáng tạo tại Lý thuyết Toán 10 CTST đồng thời tại chuyên mục Giải Toán 10 Chân trời sáng tạo Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn luyện tại nhà.
Xem thêm bài viết khác

Toán 10 Bài 2: Xác suất của biến cố

Toán 10 Bài 1: Không gian mẫu và biến cố

Toán 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ

Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ

Toán 10 Bài 1: Tọa độ của vectơ

Toán 10 Bài 3: Nhị thức Newton


































