Bài 8 trang 100 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

1 Đánh giá

GiaiToan xin giới thiệu tới các em Bài 8 trang 100 Toán 10 Tập 1 SGK Cánh Diều. Bài học hôm nay nhằm hướng dẫn các em trả lời câu hỏi bài tâp cuối chương 4 môn Toán cụ thể, chi tiết giúp các em ôn tập, rèn luyện nâng cao kỹ năng giải các bài tập Toán lớp 10. Dưới đây là nội dung chính, các em tham khảo nhé

Bài 8 trang 100 Toán 10 Tập 1

Đề bài

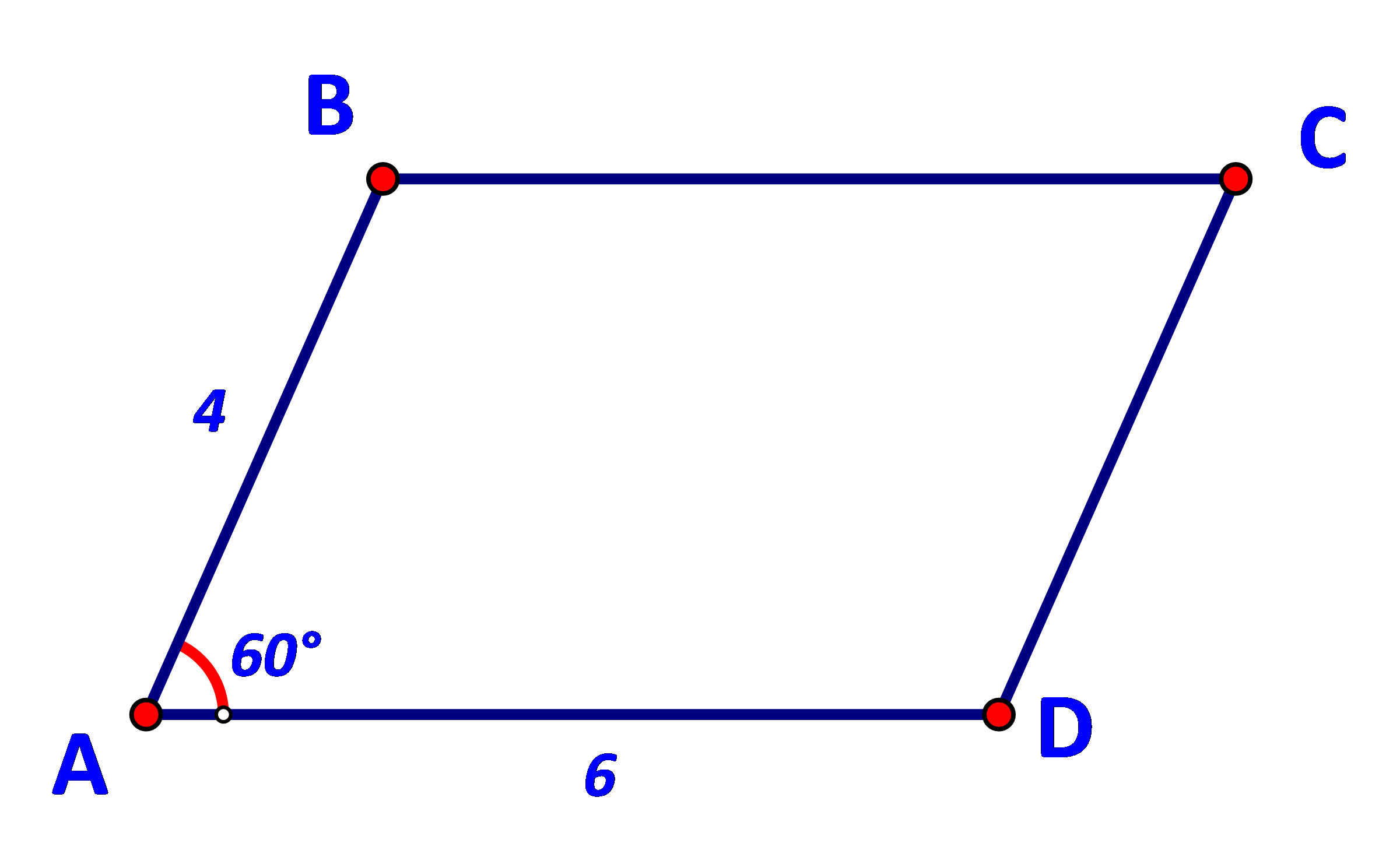
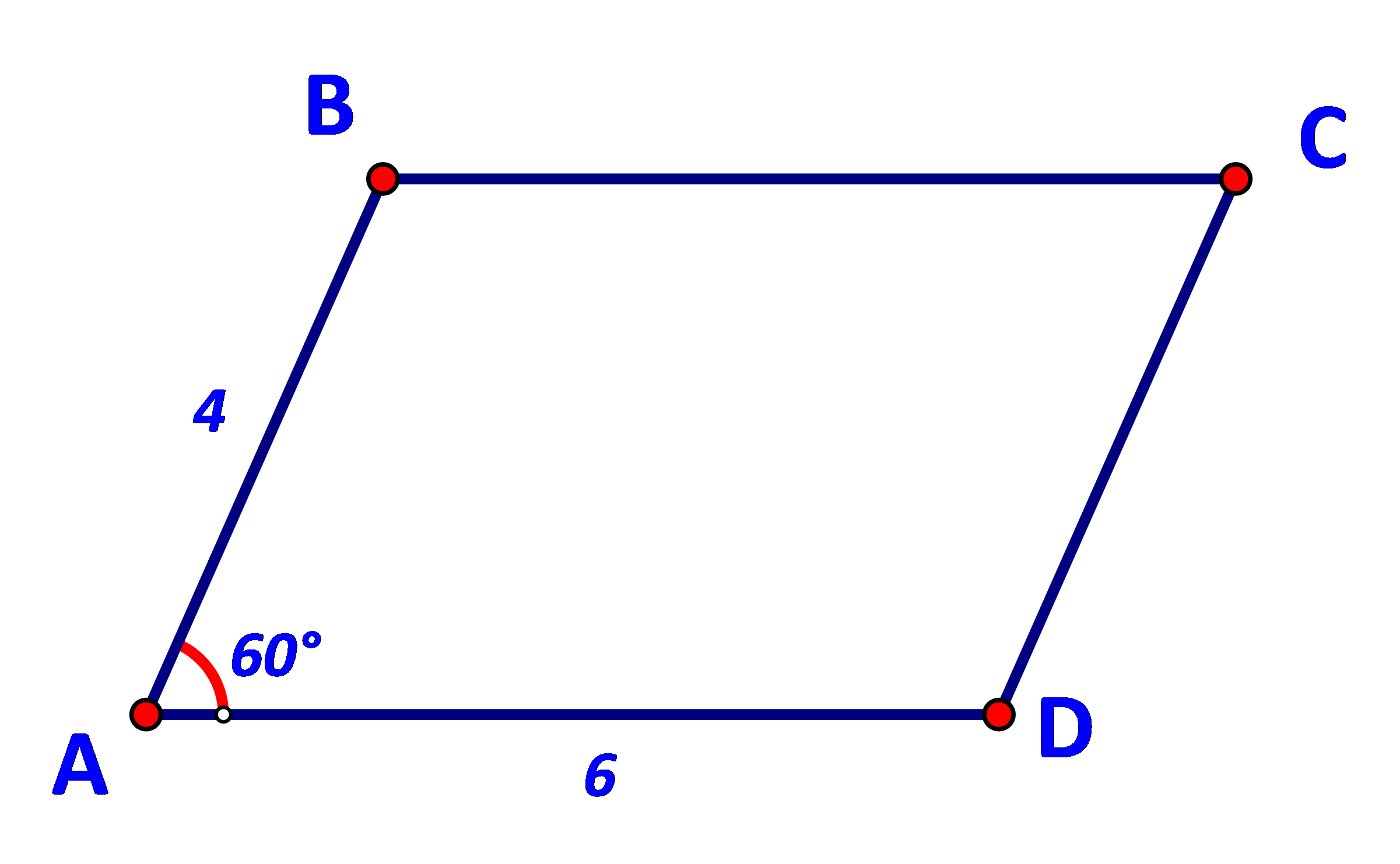
Cho hình bình hành ABCD có $AB = 4, AD = 6, \widehat {BAD} = {60^o}$ (Hình 73).

a) Biểu thị các vecto $\overrightarrow {BD} ,\overrightarrow {AC}$ theo $\overrightarrow {AB} ,\overrightarrow {AD} .$

b) Tính các tích vô hướng $\overrightarrow {AB} .\overrightarrow {AD} ,\;\overrightarrow {AB} .\overrightarrow {AC} ,\;\overrightarrow {BD} .\overrightarrow {AC} .$

c) Tính độ dài các đường chéo BD,AC.

Bài 8 trang 100 Toán 10 Tập 1

Phương pháp giải

+) ABCD là hình bình hành thì $\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .$

+) Tính $\overrightarrow {AB} .\overrightarrow {AD}$ bằng công thức $\overrightarrow {AB} .\overrightarrow {AD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos (\overrightarrow {AB} ,\overrightarrow {AD} )$

$\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} )$ (tính chất phân phối)

+) Tính BD, AC bởi định lí cosin: $B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A$

Lời giải chi tiết

Bài 8 trang 100 Toán 10 Tập 1

a) $\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .$

b) $\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.$

$\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}$

c) Áp dụng định lí cosin cho tam giác ABD ta có:

$\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}$

Áp dụng định lí cosin cho tam giác ABC ta có:

$\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}$

>>> câu hỏi cùng bài:

Bài 8 trang 100 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, củng cố kiến thức cũng như nâng cao kỹ năng giải các dạng bài tập cuối chương 4. Từ đó chuẩn bị tôt cho bài thi giữa học kì và cuối học kì lớp 10 môn Toán. Chúc các em học tốt, ngoài việc tham khảo tài liệu trên, các em có thể tham khảo thêm các dạng bài Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều tập 1 do GiaiToan biên soạn và đăng tải nhé.

Chia sẻ bởi: