Bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

1 Đánh giá

Bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan sưu tầm và đăng tải. Hướng dẫn các em trả lời câu hỏi trong bài chi tiết, ngắn gọn giúp các em ôn tập, rèn luyện kỹ năng giải bài tập cuối chương 3. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

Bài 7 trang 61 Toán 10 Tập 1

Đề bài

Giải các bất phương trình sau:

$a)\ 2{x^2} + 3x + 1 \ge 0$

$b)\ - 3{x^2} + x + 1 > 0$

$c)\ 4{x^2} + 4x + 1 \ge 0$

$d)\ - 16{x^2} + 8x - 1 < 0$

$e)\ 2{x^2} + x + 3 < 0$

$g)\ - 3{x^2} + 4x - 5 < 0$

Phương pháp giải

Giải bất phương trình dạng $f\left( x \right) > 0$ .

Bước 1: Xác định dấu của hệ số a và tìm nghiệm của $f\left( x \right)$ (nếu có)

Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho $f\left( x \right)$ mang dấu “+”

Bước 3: Các bất phương trình bậc hai có dạng $f\left( x \right) < 0,f\left( x \right) \ge 0,f\left( x \right) \le 0$ được giải bằng cách tương tự.

Lời giải chi tiết

$a)\ 2{x^2} + 3x + 1 \ge 0$

Tam thức bậc hai $f\left( x \right) = 2{x^2} + 3x + 1$ có 2 nghiệm phân biệt $x = - 1,x = \frac{{ - 1}}{2}$

hệ số a = 2 > 0

Ta có bảng xét dấu f(x) như sau:

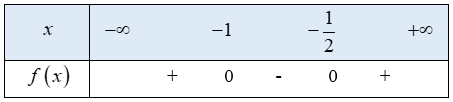
Bài 7 trang 61 Toán 10 Tập 1

Từ bảng xét dấu ta thấy $f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.$

Vậy tập nghiệm của bất phương trình là $\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)$

$b)\ - 3{x^2} + x + 1 > 0$

Tam thức bậc hai $f\left( x \right) = - 3{x^2} + x + 1$ có 2 nghiệm phân biệt $x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}$

Hệ số a = - 3 < 0

Ta có bảng xét dấu f(x) như sau:

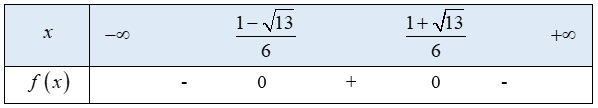
Bài 7 trang 61 Toán 10 Tập 1

Từ bảng xét dấu ta thấy $f\left( x \right) > 0 \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}$

Vậy tập nghiệm của bất phương trình là $\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)$

$c)\ 4{x^2} + 4x + 1 \ge 0$

Tam thức bậc hai $f\left( x \right) = 4{x^2} + 4x + 1$ có nghiệm duy nhất $x = \frac{{ - 1}}{2}$

hệ số a = 4 > 0

Ta có bảng xét dấu f(x) như sau:

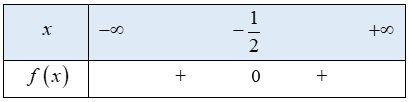
Bài 7 trang 61 Toán 10 Tập 1

Từ bảng xét dấu ta thấy $f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}$

Vậy tập nghiệm của bất phương trình là $\mathbb{R}$

$d)\ - 16{x^2} + 8x - 1 < 0$

Tam thức bậc hai $f\left( x \right) = - 16{x^2} + 8x - 1$ có nghiệm duy nhất $x = \frac{1}{4}$

hệ số a = - 16 < 0

Ta có bảng xét dấu f(x) như sau:

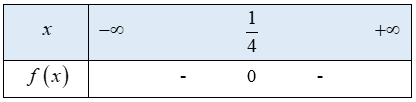
Bài 7 trang 61 Toán 10 Tập 1

Từ bảng xét dấu ta thấy $f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}$

Vậy tập nghiệm của bất phương trình là $\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}$

$e)\ 2{x^2} + x + 3 < 0$

Ta có $\Delta = {1^2} - 4.2.3 = - 23 < 0$ và có a = 2 > 0

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho $2{x^2} + x + 3$ mang dấu “-” là $\emptyset$

Vậy tập nghiệm của bất phương trình $2{x^2} + x + 3 < 0$ là $\emptyset$

$g)\ - 3{x^2} + 4x - 5 < 0$

Tam thức bậc hai $f\left( x \right) = - 3{x^2} + 4x - 5$ có $\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0$ và có $a = - 3 < 0$

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho $- 3{x^2} + 4x - 5$ mang dấu “-” là $\mathbb{R}$

Vậy tập nghiệm của bất phương trình $- 3{x^2} + 4x - 5 < 0$ là $\mathbb{R}$

>>> Câu hỏi cùng bài:

>>> Bài tiếp theo: Bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều

Bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, qua đó ôn tập, rèn luyện thêm kỹ năng giải bài Toán lớp 10 từ đó chuẩn bị tốt cho các bài kiểm tra giữa học kì, cuối kì sắp tới. Chúc các em học tốt ngoài ra các em có thể tham khảo thêm các dạng bài tập Toán lớp 10 do GiaiToan giải và biên tập nhé.

Chia sẻ bởi: