Hoạt động 9 trang 69 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

2 Đánh giá

Hoạt động 9 trang 69 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan sưu tầm và đăng tải. Bài tập bao gồm câu hỏi trong chương IV bài 1: Giá trị lượng giác của một góc từ 0⁰ đến 180⁰. Định lý côsin và định lý sin trong tam giác cùng đáp án sẽ là tài liệu hữu ích cho các em so sánh đánh giá kết quả. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

Hoạt động 9 trang 69 Toán 10 Tập 1

Đề bài:

Hoạt động 9 trang 69 Toán lớp 10 Tập 1: Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, $\widehat{B A C}=\alpha$ . Kẻ đường kính BD của đường tròn (O).

Cho α là góc nhọn. Chứng minh:

a) $\widehat{B D C}=\alpha$

b) $\frac{a}{\sin \alpha}=2 R \text {. }$

Lời giải:

Do α là góc nhọn ta vẽ được hình như sau:

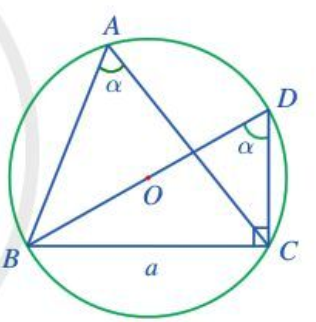
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a

a) Trong đường tròn (O) có góc BAC và góc BDC là các góc nội tiếp cùng chắn cung nhỏ BC.

Do đó: $\widehat{B D C}=\widehat{B A C}=\alpha$

Vậy $\widehat{B D C}=\alpha$

b) Xét tam giác BDC, ta có $\widehat{B D C}=\alpha$

Vì BD là đường kính của đường tròn (O) nên $\widehat{B C D}=90^{0}$ .

Do đó: $Sin \widehat{B D C}=\frac{BC}{BD}$ , tức là $Sin\ \alpha =\frac{a}{2R}$ hay $\frac{a}{sin\ \alpha}=2R$

>>> Câu hỏi cùng bài:

>>> Câu hỏi tiếp theo: Hoạt động 10 trang 69 Toán 10 Tập 1 SGK Cánh Diều

Hoạt động 9 trang 69 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan đã chia sẻ xong trên đây. Với phần hướng dẫn trả lời chi tiết sẽ là tài liệu hữu ích cho các em tham khảo, qua đó rèn luyện thêm các dạng bài toán lớp 10 chương 4: Hệ thức trong tam giác. Vectơ. Chúc các em học tốt ngoài ra các em có thể tham khảo thêm các dạng bài tập Toán lớp 10 do GiaiToan giải và biên tập nhé.

Chia sẻ bởi: