Bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều Giải SGK Toán 10

3 Đánh giá

GiaiToan xin giới thiệu tới các em Bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều. Hướng dẫn các em có thêm tài liệu tham khảo chi tiết, ngắn gọn giúp các em ôn tập, rèn luyện kỹ năng giải bài Toán lớp 10. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

Bài 4 trang 59 Toán 10 Tập 1

Đề bài

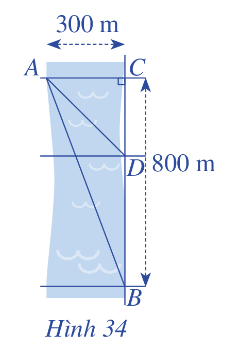
Một người đứng ở điểm A trên một bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.

Bài 4 trang 59 Toán 10 Tập 1

Phương pháp giải

- Gọi khoảng cách từ C đến D là x m (x>0)

- Biểu diễn DB, AD theo x.

- Biểu diễn đi từ A đến D và đi từ D đến B theo x.

- Lập phương trình và giải.

Lời giải chi tiết

Đổi 300 m =0,3 km, 800 m = 0,8 km

7,2 phút =0,12(h)

Gọi khoảng cách từ C đến D là x (km) (0,8>x>0)

Khi đó, DB=0,8-x (km)

Theo định lý Py-ta-go ta có: $AD = \sqrt {A{C^2} + C{D^2}} = \sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} (km)$

Thời gian đi từ A đến D là: $\frac{{\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} }}{6}\left( h \right)$

Thời gian đi từ D đến B là: $\frac{{0,8 - x}}{{10}}\left( h \right)$

Tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút nên ta có phương trình:

$\begin{array}{l}\frac{{\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} }}{6} + \frac{{0,8 - x}}{{10}} = 0,12\\ \Leftrightarrow \sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} .5 + 3.\left( {0,8 - x} \right) = 0,12.30\\ \Leftrightarrow 5.\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} - 3x - 1,2 = 0\\ \Leftrightarrow 5.\sqrt {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} = 3x + 1,2\\ \Leftrightarrow 25.\left[ {0,{3^2} + {{\left( {0,8 - x} \right)}^2}} \right] = {\left( {3x + 1,2} \right)^2}\\ \Leftrightarrow 25.\left( {{x^2} - 1,6x + 0,73} \right) = 9{x^2} + 7,2x + 1,44\\ \Leftrightarrow 16{x^2} - 47,2x + 16,81 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{59 + 30\sqrt 2 }}{{40}} > 0,8\left( {ktm} \right)\\x = \frac{{59 - 30\sqrt 2 }}{{40}} \approx 0,414\left( {tm} \right)\end{array} \right.\end{array}$

Ta bình phương được do $x > 0 \Rightarrow 3x + 1,2 > 0$

Vậy khoảng cách từ vị trí C đến D là 414m.

>>>> Câu hỏi cùng bài:

>> Câu hỏi tiếp theo: Bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều

Bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, qua đó rèn luyện kỹ năng giải bài tập chương III bài 4: Hai dạng phương trình quy về phương trình bậc hai. Chúc các em học tốt ngoài ra các em có thể tham khảo thêm các dạng bài tập Toán lớp 10 do GiaiToan giải và biên tập nhé.

Chia sẻ bởi: