Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn - Toán lớp 7 Kết nối tri thức Toán lớp 7 bài 5 - Sách KNTT

1 Đánh giá

Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn - Toán lớp 7 Kết nối tri thức được GiaiToan biên soạn và đăng tải. Nhằm giúp học sinh lớp 7 củng cố, ôn tập kiến thức lý thuyết Toán 7 Chương 1: Số hữu tỉ. Mời thầy cô và các em học sinh tham khảo tài liệu

Lý thuyết toán lớp 7 bài 5: Làm quen với số thập phân vô hạn tuần hoàn

1. Số thập phân vô hạn tuần hoàn
2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước
3. Bài tập Làm quen với số thập phân vô hạn tuần hoàn
4. Giải Toán 7 bài 5 Làm quen với số thập phân vô hạn tuần hoàn
5. Luyện tập làm quen với số thập phân vô hạn tuần hoàn

1. Số thập phân vô hạn tuần hoàn

Số thập phân vô hạn tuần hoàn là số thập phân có phần thập phân lặp lại và phần lặp lại vô hạn.
Chu kì của số thập phân vô hạn tuần hoàn là phần được lặp lại vô hạn lần.
Số thập phân hữu hạn là số thập phân như 0,8; 1,25; …

Ví dụ:

+ Khi chia 5 cho 18 được thương là 0,2777…, chữ số 7 được lặp lại mãi. Nên $\frac{5}{18}=0,2777 \ldots=0,2(7)$ là số thập phân vô hạn tuần hoàn với chu kì là 7.

Số thập phân vô hạn tuần hoàn

+ Phân số $\frac{7}{22}=0,31818 \ldots=0,3(18)$ là số thập phân vô hạn tuần hoàn với chu kì là 18.

+ Phân số $-\frac{65}{888}=-0,073198198 \ldots=-0,073(198)$ là số thập phân vô hạn tuần hoàn với chu kì là 198.

Chú ý:

Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ: Số $\frac{3}{4}=0,75 ;-\frac{11}{12}=-0,91(6)$

2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước

Khi làm tròn số đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.

Ví dụ:

+ Làm tròn a = 37,222… đến hàng đơn vị thì được kết quả là 37. Ta viết 37,222… ≈ 37. Ta cũng nói rằng 37 là kết quả làm tròn của a = 37,222… với độ chính xác là 0,5.

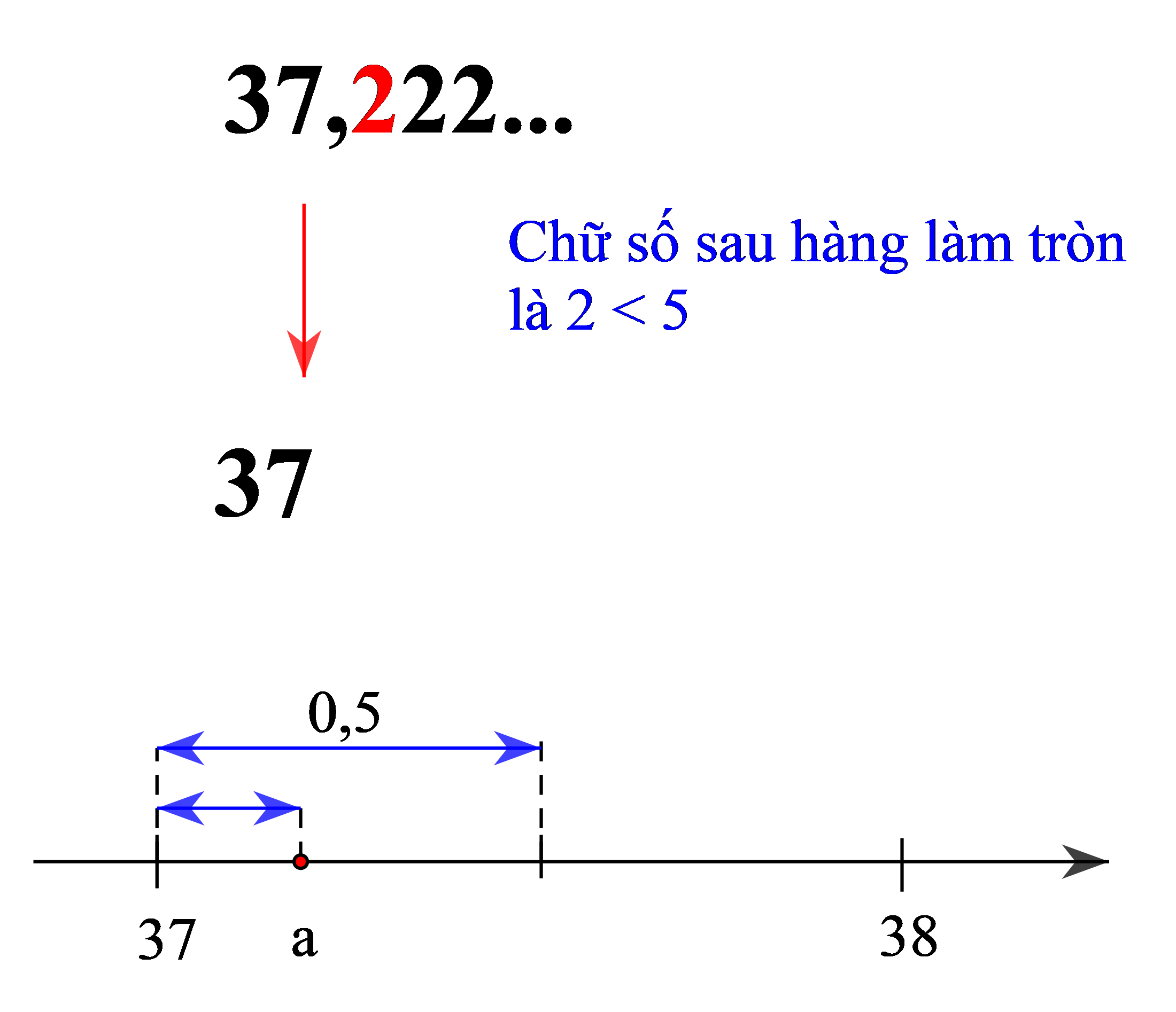
Làm tròn số thập phân căn cứ vào độ chính xác cho trước

+ Làm tròn số 6,5858… đến hàng phần mười ta được kết quả 6,5858… ≈ 6,6 với độ chính xác là 0,05.

+ Để làm tròn số 19,1094 với độ chính xác là 5, ta làm tròn đến hàng chục. Ta được 19,1094 ≈ 20.

Chú ý:

Muốn làm tròn số thập phân với độ chính xác cho trước, ta có thể xác định hàng làm tròn thích hợp bằng cách sử dụng bảng dưới đây.

Hàng làm tròn	Độ chính xác
Trăm	50
Chục	5
Đơn vị	0,5
Phần mười	0,05
Phần trăm	0,005

Đọc thêm

Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân hữu hạn. Ví dụ:

$\frac{3}{50}=\frac{3}{2.5^2}=\frac{6}{100}=0,06$

Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân vô hạn tuần hoàn. Ví dụ: $\frac{1}{6}=\frac{1}{23}=0,1666 \ldots$
Mỗi số thập phân vô hạn tuần hoàn biểu diễn một số hữu tỉ. Ví dụ:

$0,(1)=\frac{1}{9} ; 0,(01)=\frac{1}{99} ; 0,(21)=\frac{21}{99} ; 0,(9)=1$

3. Bài tập Làm quen với số thập phân vô hạn tuần hoàn

Bài 1. Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn?

a) 0,202

b) 0,9(86)

c) – 1,(3)

d) – 6,25

e) 5,343(12)

f) 0,30300300030000… (viết liên tiếp các số 30; 300; 3000; 30 000; … sau dấu phẩy).

Hướng dẫn giải

a) 0,202 là số thập phân hữu hạn.

b) 0,9(86) có số 86 ở phần thập phân được lặp lại mãi nên 0,9(86) là số thập phân vô hạn tuần hoàn.

c) – 1,(3) có số 3 ở phần thập phân được lặp lại mãi nên – 1,(3) là số thập phân vô hạn tuần hoàn.

d) – 6,25 là số thập phân hữu hạn.

e) 5,343(12) có số 12 ở phần thập phân được lặp lại mãi nên 5,343(12) là số thập phân vô hạn tuần hoàn.

f) 0,30300300030000… (viết liên tiếp các số 30; 300; 3000; 30 000; … sau dấu phẩy) không là số thập phân hữu hạn, cũng không là số thập phân vô hạn tuần hoàn vì phần thập phân không được lặp lại đều đặn.

Bài 2. Sử dụng chu kì, hãy viết gọn các số thập phân vô hạn tuần hoàn dưới đây:

a) 0,010101…

b) – 0,13888…

c) 5,3022121…

d) 0,1636363…

Hướng dẫn giải

a) Ta thấy số 0,010101… phần thập phân có chu kỳ là 01 nên 0,010101… = 0,(01)

b) Ta thấy số – 0,13888… phần thập phân có chu kỳ là 8 nên – 0,13888… = – 0,13(8)

c) Ta thấy số 5,3022121… phần thập phân có chu kỳ là 21 nên 5,3022121… = 5,302(21)

d) Ta thấy số 0,1636363… phần thập phân có chu kỳ là 63 nên 0,1636363… = 0,1(63)

Bài 3. Làm tròn các số 1,41421…; 1,9(81); 7,(35).

a) đến chữ số thập phân thứ ba;

b) với độ chính xác là 0,005.

Hướng dẫn giải

a) đến chữ số thập phân thứ ba

Số 1,41421… có chữ số sau chữ số thập phân thứ ba là 2 < 5.

Nên 1,41421… ≈ 1,414

Số 1,9(81) = 1,98181… có chữ số sau chữ số thập phân thứ ba là 8 > 5.

Nên 1,9(81) ≈ 1,982

Số 7,(35) = 7,3535… có chữ số sau chữ số thập phân thứ ba là 5 = 5.

Nên 7,(35) ≈ 7,354

b) với độ chính xác là 0,005 tức là làm tròn đến hàng phần trăm

Số 1,41421… có chữ số sau hàng phần trăm là 4 < 5.

Nên 1,41421… ≈ 1,41

Số 1,9(81) = 1,98181… có chữ số sau hàng phần trăm là 1 < 5.

Nên 1,9(81) ≈ 1,98

Số 7,(35) = 7,3535… có chữ số sau hàng phần trăm là 3 < 5.

Nên 7,(35) ≈ 7,35.

4. Giải Toán 7 bài 5 Làm quen với số thập phân vô hạn tuần hoàn

Giải bài tập SGK Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn

>>> Bài tiếp theo: Lý thuyết Toán lớp 7 bài 6: Số vô tỉ. Căn bậc hai số học - KNTT

>>> Bài trước: Lý thuyết Thứ tự thực hiện các phép tính. Quy tắc chuyển vế lớp 7

5. Luyện tập làm quen với số thập phân vô hạn tuần hoàn

-------------------------------------------------------

Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn - Toán lớp 7 Kết nối tri thức được GiaiToan chia sẻ trên đây. Hy vọng sẽ giúp ích cho các em nắm chắc kiến thức cơ bản Toán lớp 7, từ đó áp dụng tốt vào giải các dạng bài tập toán Chương 1: Tập hợp các số hữu tỉ cũng như các bài kiểm tra quan trọng lớp 7. Chúc các em học tốt, ngoài việc tham khảo lý thuyết bài 5 các em có thể tham khảo thêm các dạng bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 1 KNTT do GiaiToan biên soạn và đăng tải nhé.