Toán 7 Bài 25: Đa thức một biến Toán 7 sách Kết nối tri thức

Lý thuyết bài 25: Đa thức một biến - Toán lớp 7 Kết nối tri thức trang 25 SGK được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm tóm tắt lý thuyết kèm theo bài tập để các em ôn tập, nắm chắc kiến thức của bài từ đó học tốt môn Toán lớp 7. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

A. Lý thuyết Đa thức một biến

1. Đa thức một biến

• Đa thức một biến là tổng của những đơn thức của cùng một biến.

• Một số được coi là một đa thức một biến.

• Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó.

Ví dụ 1: Đa thức 5x⁵ + 4x³ - 2x² + x là đa thức một biến (biến x); bậc của đa thức là 5.

Ví dụ 2: Cho đa thức sau: 5x⁷ - 7x⁶ + 5x⁵ - 4x⁴ + 7x⁶ - 3x² + 1 - 5x⁷ - 3x⁵

Bậc của đa thức đã cho là bao nhiêu?

Hướng dẫn giải:

Thu gọn đa thức ta được:

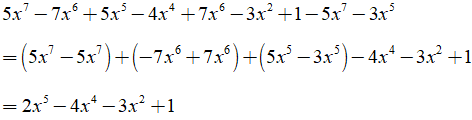
Đa thức đã cho có bậc là 5.

2. Sắp xếp một đa thức một biến

Để thuận lợi cho việc tính toán đối với các đa thức một biến, người ta thường sắp xếp các hạng tử của chúng theo lũy thừa tăng hoặc giảm của biến.

Ví dụ 1: Đối với đa thức P(x) = 6x + 3 - 6x² + x³ + 2x⁴

+ Khi sắp xếp các hạng tử của nó theo lũy thừa giảm của biến, ta được:

P(x) = 2x⁴ + x³ - 6x² + 6x + 3

+ Khi sắp xếp các hạng tử của nó theo lũy thừa tăng của biến, ta được:

P(x) = 3 + 6x - 6x² + x³ + 2x⁴

Nhận xét:

Mọi đa thức bậc 2 của biến x, sau khi đã sắp xếp các hạng tử của chúng theo lũy thừa giảm của biến, đều có dạng: ax² + bx + c

Trong đó a,b,c là các số cho trước và a ≠ 0.

Chú ý:

+ Để sắp xếp các hạng tử của một đa thức, trước hết ta phải thu gọn đa thức đó.

+ Những chữ đại diện cho các số xác định cho trước được gọi là hằng số.

Ví dụ 2: Cho đa thức P(x) = 2 + 5x² - 3x³ + 4x - 2x - x³ + 6x⁵. Thu gọn và sắp xếp đa thức

P(x) = 2 + 5x² - 3x³ + 4x² - 2x - x³ + 6x⁵ = 6x⁵ + (-3x³ - x³) + (5x² + 4x²) - 2x + 2 = 6x⁵ - 4x³ + 9x² - 2x + 2

3. Hệ số

Hệ số của lũy thừa bậc 0 của biến gọi là hệ số tự do; hệ số của lũy thừa cao nhất của biến gọi là hệ số cao nhất.

Ví dụ: Các hệ số của đa thức 6x⁵ - x⁴ + 5x² - x + 2 là 6; -1; 5; -1; 2

Hệ số tự do là: 2

Hệ số cao nhất là: 6

B. Bài tập Đa thức một biến

Bài 1: Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm dần của biến

a) 2x³ - x⁵ + 3x⁴ + x² - (1/2)x³ + 3x⁵ - 2x² - x⁴ + 1

b) x⁷ - 3x⁴ + 2x³ - x² - x⁴ - x + x⁷ - x³ + 5

Hướng dẫn giải:

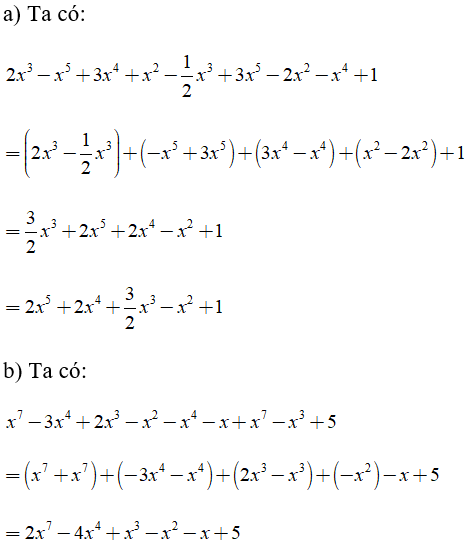
Bài 2: Tính giá trị của các biểu thức sau:

a) x + x² + x³ + x⁴ + .... + x⁹⁹ + x¹⁰⁰ tại x = -1

b) x² + x⁴ + x⁶ + .... + x⁹⁸ + x¹⁰⁰ tại x = -1

Hướng dẫn giải:

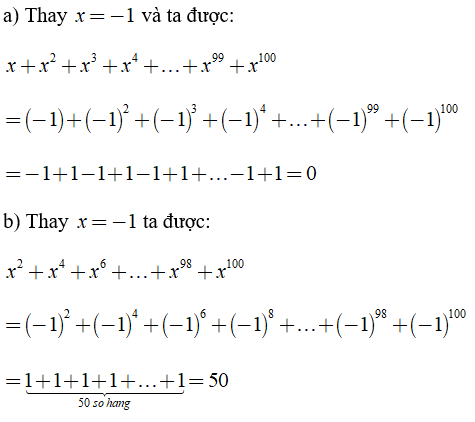
>>> Bài tiếp theo: Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

>>> Bài trước: Toán 7 Bài 24: Biểu thức đại số

Toán 7 Bài 25: Đa thức một biến được GiaiToan chia sẻ trên đây. Với phần lý thuyết này sẽ là tài liệu hữu ích cho các em tham khảo, từ đó áp dụng tốt vào giải bài tập biểu thức đại số. Chúc các em học tốt, mời các em tham khảo thêm các dạng bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 2 KNTT do GiaiToan biên soạn để ôn tập nhé. Chúc các em học tốt và đạt kết quả cao!.