Giaitoan.com Toán 7 Lý thuyết Toán 7 KNTT

Toán 7 Bài 23: Đại lượng tỉ lệ nghịch Toán 7 sách Kết nối tri thức

Nội dung
  • 2 Đánh giá

Lý thuyết bài 23: Đại lượng tỉ lệ nghịch - Toán lớp 7 Kết nối tri thức trang 15 SGK được GiaiToan biên soạn và đăng tải. Tài liệu này giúp các em nắm được kiến thức cần nhớ đồng thời làm quen với các dạng bài toán thường gặp. Dưới đây là nội dung bài chi tiết, các em cùng tham khảo nhé.

Lý thuyết Toán 7 bài 23: Đại lượng tỉ lệ nghịch

1. Các kiến thức cần nhớ

Định nghĩa tỉ lệ nghịch

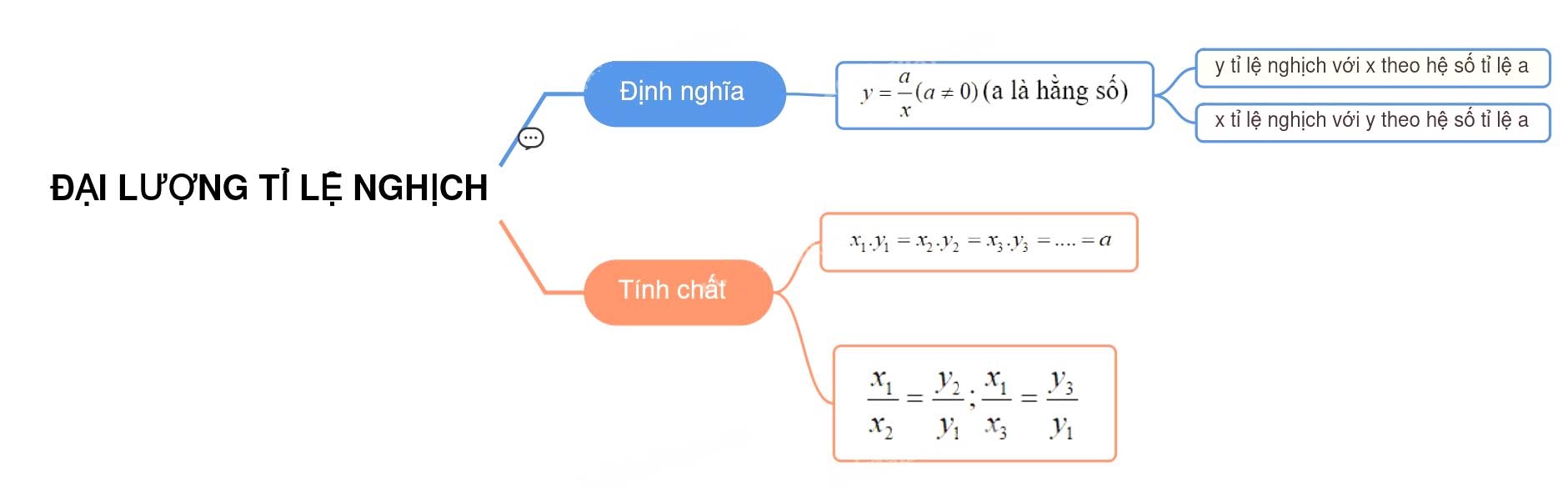
+ Nếu đại lượng y liên hệ với đại lượng x theo công thức y = \dfrac{a}{x} hay xy = a (với a là hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

+ Khi đại lượng y tỉ lệ nghịch với đại lượng x thì x cũng tỉ lệ nghịch với y và ta nói hai đại lượng đó tỉ lệ nghịch với nhau.

Ví dụ: Nếu y = \dfrac{2}{x} thì y tỉ lệ nghịch với x theo hệ số tỉ lệ là 2.

Chú ý: Khi y tỉ lệ nghịch với x theo hệ số tỉ lệ a, ta cũng nói x tỉ lệ nghịch với y theo hệ số tỉ lệ a

Tính chất

* Nếu hai đại lượng tỉ lệ nghịch với nhau thì:

+ Tích hai giá trị tương ứng của chúng luôn luôn không đổi.

+ Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia.

* Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ a thì:

{x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = ... = a

\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{{{y_2}}}{{{y_1}}};\dfrac{{{x_1}}}{{{x_3}}} = \dfrac{{{y_3}}}{{{y_1}}};...

2. Các dạng toán thường gặp

Dạng 1: Bảng giá trị tương ứng của hai đại lượng tỉ lệ nghịch

Phương pháp:

+ Xác định hệ số tỉ lệ a.

+ Dùng công thức y = \dfrac{a}{x} hoặc x = \dfrac{a}{y} để tìm các giá trị tương ứng của x và y.

Dạng 2: Xét tương quan tỉ lệ nghịch giữa hai đại lượng khi biết bảng các giá trị tương ứng của chúng

Phương pháp:

Xét xem tất cả các tích các giá trị tương ứng của hai đại lượng có bằng nhau không?

Nếu bằng nhau thì hai đại lượng tỉ lệ nghịch.

Nếu không bằng nhau thì hai đại lượng không tỉ lệ nghịch.

Dạng 3: Bài toán về các đại lượng tỉ lệ nghịch

Phương pháp:

+ Xác định rõ các đại lượng có trên đề bài.

+ Xác định tương quan tỉ lệ nghịch giữa hai đại lượng.

+ Áp dụng tính chất về tỉ số các giá trị của hai đại lượng tỉ lệ nghịch và tính chất tỉ lệ thức để giải bài toán.

Dạng 4: Chia một số thành những phần tỉ lệ nghịch với các số cho trước

Phương pháp:

Giả sử chia số M thành ba phần x;y;z tỉ lệ nghịch với các số a,b,c cho trước. Ta có

ax = by = cz hay \dfrac{x}{{\dfrac{1}{a}}} = \dfrac{y}{{\dfrac{1}{b}}} = \dfrac{z}{{\dfrac{1}{c}}}.

Như vậy để chia số M thành các phần tỉ lệ nghịch với các số a,b,c (khác 0), ta chỉ cần chia số M thành các phần tỉ lệ thuận với các số \dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c} (đã biết cách làm).

Toán 7 Bài 23: Đại lượng tỉ lệ nghịch

3. Bài tập Đại lượng tỉ lệ nghịch

>>> Bài tiếp theo: Toán 7 Bài 24: Biểu thức đại số

>>> Bài trước: Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Toán 7 Bài 23: Đại lượng tỉ lệ nghịch được GiaiToan chia sẻ trên đây. Hy vọng với tóm tắt lý thuyết này sẽ giúp các em nắm được trọng tâm của bài, từ đó áp dụng tốt vào giải các dạng bài toán về đại lượng tỉ lệ thuận. Ngoài ra, để việc học toán của các em được tốt hơn, các em tham khảo thêm các bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 2 KNTT do GiaiToan biên soạn để ôn tập nhé. Chúc các em học tốt.

  • 413 lượt xem
Chia sẻ bởi: Đinh Thị Nhàn
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Xem thêm bài viết khác

    Xem thêm Lý thuyết Toán 7 KNTT

    Chủ đề liên quan

    Lý thuyết Toán 7 Sách KNTT