Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán 7 sách Kết nối tri thức

a) Đường trung trực của tam giác

Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác. Trên (Hình bên) là đường trung trực ứng với cạnh BC của tam giác ABC.

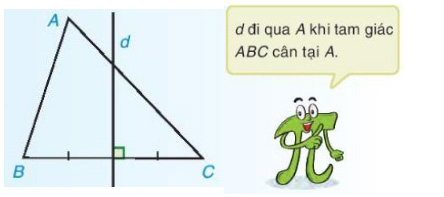
b) Sự đồng quy của ba đường trung trực

Định lí 1

Chẳng hạn, trong tam giác ABC (Hình sau), các đường trung trực dở, m, n đồng quy tại Ovà OA = OB = OG.

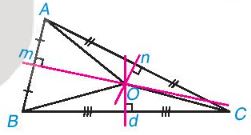
Nhận xét

Vì giao điểm O của ba đường trung trực trong tam giác ABC cách đều ba đỉnh của tam giác đó (OA = OB = OC) nên có một đường tròn tâm O đi qua ba đỉnh A, B, C
(Hình sau).

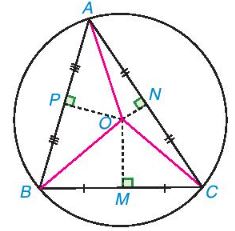
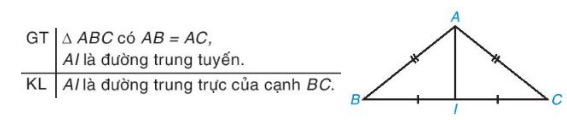
Ví dụ: Cho tam giác ABC cân tại A. Vẽ đường trung tuyến AI của tam giác ABC.

a) Chứng minh AI là đường trung trực của cạnh BC.

b) Điểm cách đều ba đỉnh của tam giác ABC có nằm trên AI không?

Giải

Chứng minh

Hai tam giác AIB và AIC có:

AB = AC(GT), IB = IC (do AI là trung tuyến); cạnh AI chung.

Do đó

Suy ra ta , mà và là hai góc kể bù nên . Do đó AI là đường trung trực của cạnh BC.

b) Do điểm cách đều ba đỉnh của tam giác ABC nằm trên đường trung trực của BC nên theo câu a, ta có điểm đó nằm trên trung tuyến AI.

a) Đường cao của tam giác

Trong Hình sau, đoạn thẳng AI kể từ đỉnh A, vuông góc với cạnh đối diện BC là một đường cao của tam giác ABC. Ta còn nói AI là đường cao xuất phát từ đỉnh A (hay đường cao ứng với cạnh BC).

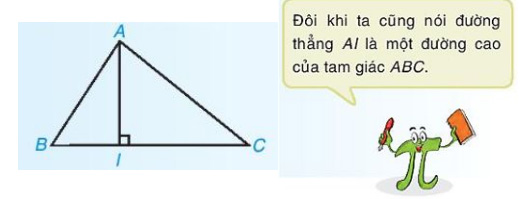
b) Sự đồng quy của ba đường cao

Định lí 2

Chẳng hạn, trong tam giác A8C (Hình sau), các đường cao AI, BJ, CK đồng quy tại H.

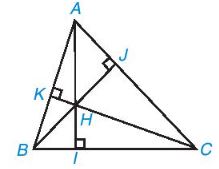
Chú ý

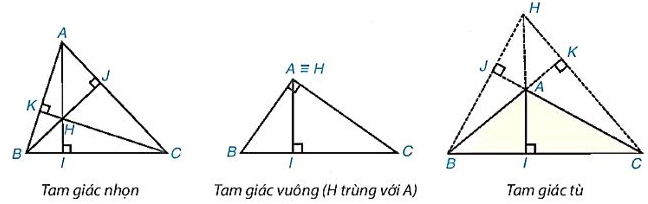
a) Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó.

b) Gọi H là trực tâm của tam giác ABC (H.9.44), ta có:

+ Khi ABC là tam giác nhọn thì H nằm bên trong tam giác.

+ Khi ABC là tam giác vuông tại A thì H trùng với A (kí hiệu là H \equiv A).

+ Khi ABC là tam giác tù thì H nằm bên ngoài tam giác.

Ví dụ: Chứng minh trong tam giác đều, trực tâm của nó cách đều đỉnh của tam giác.

Giải

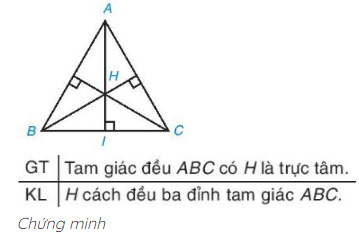
Trong tam giác ABC cân tại A, kẻ đường cao AI.

Hai tam giác vuông ABI và ACI có: AI chung, AB = AC (gt).

Do đó  (cạnh huyền - cạnh góc vuông). Suy ra BI = CI.

Vậy đường cao AI là đường trung trực của cạnh BC.

Vì tam giác đều cũng là tam giác cân tại mỗi đỉnh nên ba đường cao cũng là ba đường trung trực của nó. Vậy trực tâm H của tam giác đều cũng là giao điểm của ba đường trung trực nên nó cách đều ba đỉnh của tam giác.

Câu 1: Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.

Hướng dẫn giải

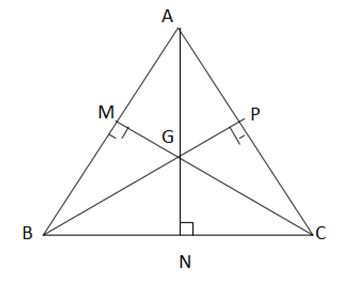
Gọi AN, CM, BP là 3 đường trung tuyến của tam giác đều ABC, giao nhau ở điểm G

Xét ∆ ANB và ∆ ANC, có:

AN chung

NB= NC

AB= AC

=>∆ ANB = ∆ ANC

=> AN hay AG là đường phân giác của

Tương tự BP hay BG là đường phân giác của

=> G cách đều 3 cạnh AB, AC, BC mag G là trọng tâm

=> G là giao điểm của 3 đường trung trực => G cách đều 3 điểm A,B,C

Câu 2: Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không?

Hướng dẫn giải

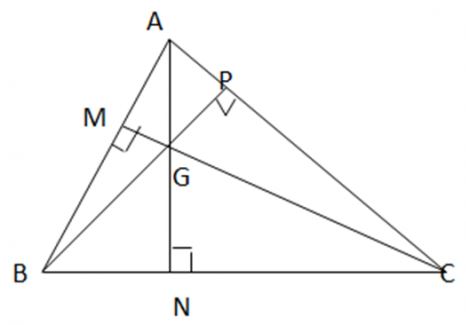
Ba đường cao BP, CM và AN đều cùng đi qua điểm G