Số nguyên a có phải là số hữu tỉ không? Vì sao? Số hữu tỉ
Tập hợp Q - Số hữu tỉ
Tập hợp Q - Tập hợp các số hữu tỉ với nội dung kiến thức khá phong phú, xuất hiện dày đặc trong một chương với số tiết học không nhiều nên một số kiến thức chỉ nói đến tính chất chứ không được làm rõ trên lớp học đó là Số nguyên là số hữu tỉ, có lẽ học sinh sẽ rất băn khoăn tại sao lại như vậy. Để giải thích cho vấn đề trên trước hết học sinh cần hiểu:
1. Số hữu tỉ là gì?
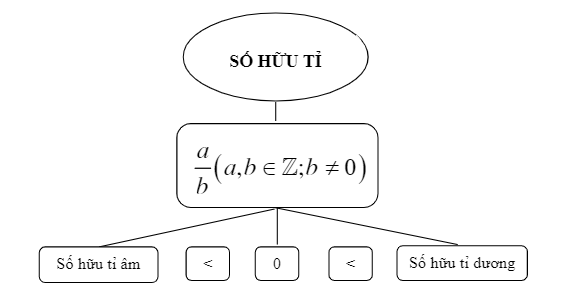
- Số hữu tỉ là số viết dưới dạng phân số ![]() với
với ![]() .
.
- Tập hợp các số hữu tỉ được kí hiệu là
Ví dụ: -3; -1,75, ![]() , … là các số hữu tỉ.
, … là các số hữu tỉ.
- Số nguyên a bất kì là một số hữu tỉ vì số nguyên a có thể viết dưới dạng ![]()
Ví dụ: Ta có 1; -3; 0 là các số hữu tỉ.
Ta có:

Nhận xét: ![]() đều là số hữu tỉ
đều là số hữu tỉ
Từ đó => Biểu đồ Ven biểu thị mối quan hệ các tập hợp số:
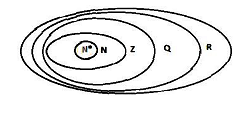
2. Biểu diễn số hữu tỉ trên trục số
- Để biểu diễn số hữu tỉ trên trục số ta làm theo các ước sau:
Bước 1: Viết số hữu tỉ dưới dạng phân số ![]()
Bước 2: Chia đoạn thẳng đơn vị thành b phần bằng nhau ta được đoạn đơn vị mới là ![]() đơn vị cũ.
đơn vị cũ.
Bước 3: Số hữu tỉ ![]() được biểu diễn bằng điểm A cách điểm 0 một đoạn bằng a đơn vị mới.
được biểu diễn bằng điểm A cách điểm 0 một đoạn bằng a đơn vị mới.
+ A nằm bên trái điểm 0 nếu là số âm.
+ A nằm bên phải điểm 0 nếu là số dương.
3. So sánh hai số hữu tỉ
- Với 2 số hữu tỉ bất kì x, y ta luôn có hoặc x = y hoặc x < y hoặc x > y.
- Để so sánh hai số hữu tỉ x, y ta làm như sau:
+) Viết x, y dưới dạng 2 phân số cùng mẫu dương: ![]()
+) So sánh tử số là các số nguyên a, b:

-----------------------------------------------------
Hy vọng tài liệu Số hữu tỉ Số vô tỉ Toán 7 sẽ giúp ích cho các bạn học sinh học nắm chắc các cách biến đổi biểu thức chứa căn đồng thời học tốt môn Toán lớp 7. Chúc các bạn học tốt, mời các bạn tham khảo! Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Lý thuyết Toán 7, Luyện tập Toán 7, Giải toán 7, ...
- Lượt xem: 2.181











































