Toán 7 Bài 28: Phép chia đa thức một biến Toán 7 sách Kết nối tri thức
Lý thuyết bài 28: Phép chia đa thức một biến - Toán lớp 7 Kết nối tri thức trang 39 SGK được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm các kiến thức cần nhớ kèm theo các dạng toán thường gặp, giúp các em nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7. Dưới đây là nội dung chi tiết, các em tham khảo nhé.
Lý thuyết Toán 7 bài 28: Phép chia đa thức một biến
1. Các kiến thức cần nhớ
Chia đa thức một biến đã sắp xếp
- Muốn chia đa thức một biến A cho đa thức một biến ![]() , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên.
, trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên.
- Với hai đa thức tùy ý A và B của một biến ![]() , tồn tại duy nhất hai đa thức Q và R sao cho A = B.Q + R
, tồn tại duy nhất hai đa thức Q và R sao cho A = B.Q + R
Trong đó R = 0 hoặc bậc của R thấp hơn bậc của B.
+ Nếu R = 0 thì phép chia A cho B là phép chia hết.
+ Nếu ![]() thì phép chia A cho B là phép chia có dư.
thì phép chia A cho B là phép chia có dư.
Ví dụ 1:
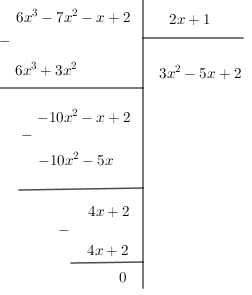
Ta viết lại ![]() . Nhận thấy số dư R = 0 nên đây là phép chia hết.
. Nhận thấy số dư R = 0 nên đây là phép chia hết.
Ví dụ 2:
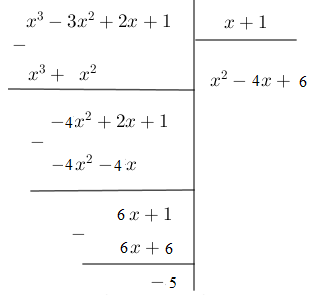
Ta viết lại ![]() . Vì
. Vì ![]() nên đây là phép chia có dư.
nên đây là phép chia có dư.
2. Các dạng toán thường gặp
Dạng 1: Tìm thương, số dư của phép chia đa thức một biến đã sắp xếp
Phương pháp:
Muốn chia đa thức một biến A cho đa thức một biếnB \ne 0 , trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên.
Dạng 2: Xác định hằng số a,b sao cho phép chia cho trước là phép chia hết.
Phương pháp:
Sử dụng tính chất phép chia hết có số dư R = 0 để tìm a,b .
Chú ý:
Ax + B = 0 với ![]()
>>> Bài tiếp theo: Toán 7 Bài 29: Làm quen với biến cố
>>> Bài trước: Toán 7 Bài 27: Phép nhân đa thức một biến
Toán 7 Bài 28: Phép chia đa thức một biến được GiaiToan chia sẻ trên đây. Hy vọng với phần tóm tắt lý thuyết này sẽ giúp ích cho các em nắm được trọng tâm của bài, từ đó áp dụng vào giải các dạng bài tập về phép nhân đa thức một biến. Chúc các em học tốt, mời các em tham khảo thêm các dạng bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 2 KNTT do GiaiToan biên soạn để ôn tập nhé. Chúc các em học tốt.
Xem thêm bài viết khác

Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Toán 7 Bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác

Toán 7 Bài 33: Quan hệ giữa ba cạnh của một tam giác

Toán 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên

Toán 7 Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Toán 7 Bài 30: Làm quen với xác suất của biến cố

Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Toán 7 Bài 25: Đa thức một biến

Toán 7 Bài 24: Biểu thức đại số

Toán 7 Bài 23: Đại lượng tỉ lệ nghịch

Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Toán 7 Bài 21: Tính chất của dãy tỉ số bằng nhau








































