Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán 7 sách Kết nối tri thức

1 Đánh giá

Lý thuyết bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác - Toán lớp 7 Kết nối tri thức trang 94 SGK được GiaiToan biên soạn và đăng tải. Bài học hôm nay gồm kiến thức cần nhớ, các bài tập minh họa có hướng dẫn giải chi tiết, giúp các em học tập và củng cố thật tốt kiến thức. Mời các em cùng tham khảo.

Lý thuyết Toán 7 bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

1. Tóm tắt lý thuyết
- 1.1. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
- 1.2. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
2. Bài tập minh họa

1. Tóm tắt lý thuyết

1.1. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

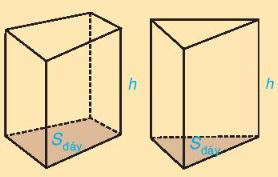
Trong hình lăng trụ đứng tam giác (tứ giác):

- Hai mặt đáy song song với nhau.

- Các mặt bên là những hình chữ nhật.

- Các cạnh bên song song và bằng nhau.

Độ dài một cạnh bên gọi là chiều cao của lăng trụ đứng.

Ví dụ: Hãy cho biết đỉnh, cạnh đáy, cạnh bên, mặt đáy, mặt bên của hình lăng trụ đứng tam giác ABC.A'B'C' trong Hình sau

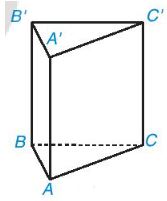
Giải

Các đỉnh: A, B, C, A', B', C'.

Các cạnh đáy: AB, BC, CA, A'B', B'C', C'A'.

Các cạnh bên: AA', BB', CC'.

Các mặt đáy là các tam giác ABC và A'B'C'.

Các mặt bên là các hình chữ nhật ABB'A', ACC'A', BCC'B'.

1.2. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

a) Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác:

${S_{xq}} = C.h$

trong đó ${S_{xq}}$ : Diện tích xung quanh của hình lăng trụ,

C: Chu vi một đáy của hình lăng trụ,

h: Chiêu cao của lăng trụ.

Ví dụ: Một quyển lịch để bàn (Hình bên dưới) gồm các tờ lịch được đặt trên một giá đỡ bằng bìa có dạng hình lăng trụ đứng tam giác. Tính diện tích bìa dùng để làm giá đỡ của quyển lịch.

Giải

Diện tích bìa dùng để làm giá đỡ của quyển lịch là diện tích xung quanh của hình lăng trụ đứng tam giá:

${S_{xq}} = C.h = \left( {20 + 20 + 7} \right).25 = 47.25 = 1175(c{m^2})$

b) Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

Tương tự như hình hộp chữ nhật, hình lập phương, thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác được tính bằng tích của diện tích đáy và chiều cao của nó.

Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác:

$V = {S_{day}}.h$

trong đó V: Thể tích của hình lăng trụ đứng,

Sđáy: Diện tích một đáy của hình lăng trụ đứng,

h: Chiêu cao của hình lăng trụ đứng.

Ví dụ: Một lăng kính được làm bằng thuỷ tinh có dạng một hình lăng trụ đứng tam giác như Hình bên dưới. Tính thể tích thuỷ tỉnh dùng để làm lăng kính.

Giải

Diện tích tam giác đáy là ${S_{day}} = \frac{1}{2}.10.8,7 = 43,5\left( {c{m^2}} \right)$

Thể tích thuỷ tinh dùng làm lăng kính là:

$V = {S_{day}}.h = 43,5.20 = 870\left( {c{m^3}} \right).$

2. Bài tập minh họa

Câu 1: Một lều chữ A dạng hình lăng trụ đứng có kích thước như hình sau. Tính diện tích vải để làm hai mái và trải đáy của lều

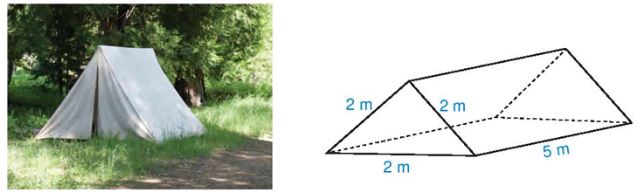
Hướng dẫn giải

Diện tích vải để làm hai mái và trải đáy của lều chính là diện tích xung quanh hình lăng trụ:

(2 + 2 + 2). 5 = 30 (m²)

Câu 2: Quan sát hình lăng trụ đứng tam giác ABC. A'B'C' và hình triển khai của nó. Hãy chỉ ra sự tương ứng giữa các mặt bên và các mặt hình chữ nhật của hình khai triển

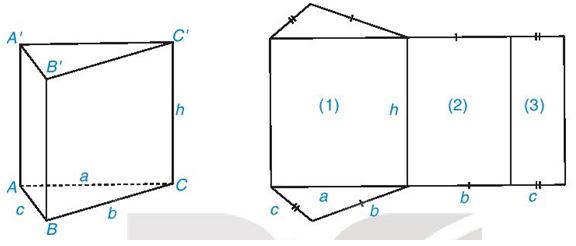
Hướng dẫn giải

Mặt bên ABB'A' tương ứng với hình chữ nhật (3)

Mặt bên BCC'B', ACC'A' lần lượt tương ứng với hình chứ nhật (1), (2).

>>> Bài trước: Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác được GiaiToan chia sẻ trên đây. Hy vọng qua bài học này các em học sinh sẽ mô tả hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác và tạo lập hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác, biết cách tính diện tích xung quanh, thể tích của hình lăng trụ đứng tam giác hình lăng trụ đứng tứ giác. Ngoài việc tham khảo lý thuyết trên đây, các em cũng đừng quên ôn tập thêm các dạng bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 1 KNTT do GiaiToan biên soạn để ôn tập nhé.