Toán 10 Bài 3: Khái niệm vectơ sách CD Giải Toán 10 sách Cánh Diều
Lý thuyết Khái niệm vectơ trang 79 sách Cánh Diều được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm lý thuyết cùng bài tập cụ thể, giúp các em nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10. Dưới đây là nội dung chi tiết, các em tham khảo nhé.
Toán 10 Bài 3: Khái niệm vectơ
1. Lý thuyết Khái niệm vectơ
Khái niệm vectơ
Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểu đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.
Định nghĩa: Vectơ là một đoạn thẳng có hướng.
Vectơ có điểm đầu A, điểm cuối B được kí hiệu là ![]() và đọc là “vectơ AB”. Để vẽ được vectơ
và đọc là “vectơ AB”. Để vẽ được vectơ ![]() ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.
ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.
Đối với vectơ ![]() ta gọi:
ta gọi:
– Đường thẳng d đi qua hai điểm A và B là giá của vectơ ![]()
– Độ dài đoạn thẳng AB là độ dài của vectơ ![]() , kí hiệu là
, kí hiệu là ![]()
Vectơ còn được kí hiệu là ![]() khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ
khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ ![]() được kí hiệu là
được kí hiệu là ![]()
Ví dụ: Vectơ ![]() có độ dài là 5, ta có thể viết như sau:
có độ dài là 5, ta có thể viết như sau: ![]()
2. Vectơ cùng phương, vectơ cùng hướng
Định nghĩa:
– Hai vectơ cùng phương: Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Ví dụ:
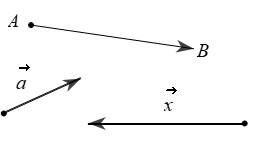
Trên hình vẽ các vectơ ![]() cùng phương với nhau.
cùng phương với nhau.
Nhận xét: Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.
Ví dụ:
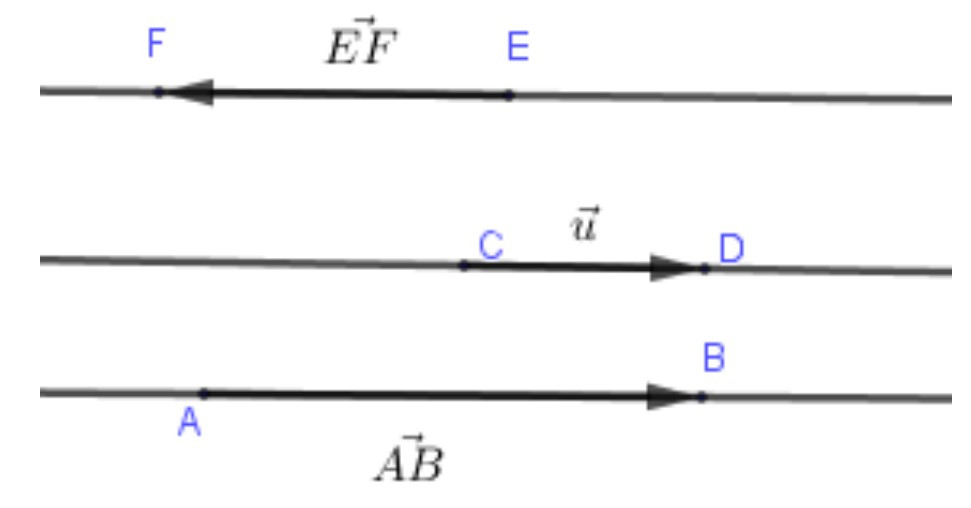
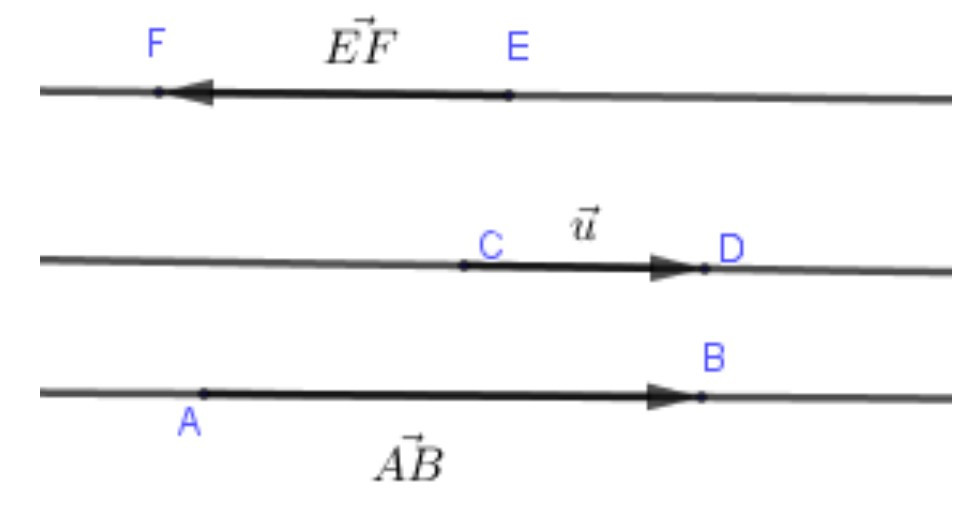
Hai vectơ ![]() và
và ![]() cùng phương và có cùng hướng đi từ trái sang phải. Ta nói hai vectơ
cùng phương và có cùng hướng đi từ trái sang phải. Ta nói hai vectơ ![]() và
và ![]() cùng hướng. Hai vectơ
cùng hướng. Hai vectơ ![]() và
và ![]() cùng phương nhưng ngược hướng nhau. Ta nói hai vectơ
cùng phương nhưng ngược hướng nhau. Ta nói hai vectơ ![]() và
và ![]() là hai vectơ ngược hướng.
là hai vectơ ngược hướng.
Ví dụ: Cho hình bình hành ABCD. Liệt kê các cặp vectơ cùng hướng và ngược hướng trong hình bình hành ABCD.
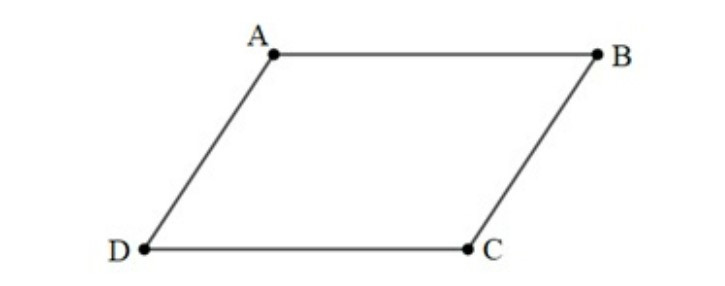
Hướng dẫn giải:
Do ABCD là hình bình hành nên ta có: AB // DC và AD // BC.
Các cặp vectơ cùng hướng: ![]() và
và ![]() ,
, ![]() và
và ![]() ,
,![]() và
và ![]() ,
, ![]() và
và ![]()
Các cặp vectơ ngược hướng: ![]() và
và ![]() ,
, ![]() và
và ![]() ,
, ![]() và
và ![]() ,
, ![]() và
và ![]()
3. Hai vectơ bằng nhau
Hai vectơ ![]() ,
, ![]() bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu:
bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: ![]() =
= ![]()
Nhận xét:
– Hai vectơ ![]() và
và ![]() được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu
được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu ![]() =
=![]()
– Khi cho trước vectơ ![]() và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho
và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho ![]() =
= ![]()
Ví dụ: Cho hình bình hành ABCD, khi đó:

Do ABCD là hình bình hành nên ta có:
![]()
Ta lại có: ![]() và
và ![]() ;
; ![]() và
và ![]() là hai cặp vectơ cùng hướng nên
là hai cặp vectơ cùng hướng nên 
4. Vectơ–không
Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.
Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là ![]() và được gọi là vectơ – không.
và được gọi là vectơ – không.
Định nghĩa: Vectơ–không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là ![]()
Ta quy ước ![]() cùng phương và cùng hướng với mọi vectơ và
cùng phương và cùng hướng với mọi vectơ và ![]()
Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi ![]() =
= ![]()
Ví dụ: Vectơ ![]() là vectơ – không và
là vectơ – không và ![]() =0
=0
5. Biểu thị một số đại lượng có hướng bằng vectơ
Trong vật lý, một số đại lượng như trọng lực, vận tốc,… là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng đó.
Ví dụ: Chọn trục tọa độ là trục Oy có chiều hướng lên trên, biểu điễn vectơ lực ![]() có điểm đặt tại gốc O trong hai trường hợp sau:
có điểm đặt tại gốc O trong hai trường hợp sau:
a) ![]() có phương thẳng đứng chiều hướng xuống
có phương thẳng đứng chiều hướng xuống
b) ![]() có phương thẳng đứng hướng lên trên
có phương thẳng đứng hướng lên trên

Ta thấy vectơ lực ![]() ở hai trường hợp cùng phương nhưng ngược hướng với nhau.
ở hai trường hợp cùng phương nhưng ngược hướng với nhau.
6. Giải Toán 10 bài 3 SGK + SBT Cánh Diều
- Giải Toán 10 Bài 3 chương 4: Khái niệm vectơ sách Cánh Diều
- Trắc nghiệm Toán 10 Bài 3: Khái niệm vectơ
>>> Bài tiếp theo: Toán 10 Bài 4: Tổng và hiệu của hai vectơ sách CD
>>> Bài trước: Toán 10 Bài 2: Giải tam giác sách CD
Toán 10 Bài 3: Khái niệm vectơ sách CD được GiaiToan chia sẻ trên đây. Với phần lý thuyết cùng bài tập kèm theo sẽ giúp các em có thêm tài liệu tham khảo, củng cố kiến thức cũng như áp dụng vào giải các bài tập về khái niệm vectơ, từ đó chuẩn bị tốt cho bài thi giữa học kì và cuối học kì môn Toán lớp 10. Ngoài tham khảo tài liệu trên các em cũng đừng quên tham khảo thêm các dạng bài tập Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều Tập 1 do GiaiToan biên soạn nhé.
Xem thêm bài viết khác

Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn sách CTST

Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách CTST

Toán 10 Bài 6: Tích vô hướng của hai vectơ sách CD

Toán 10 Bài 5: Tích của một số với một vectơ sách CD

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác sách CD

Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai sách CD

Toán 10 Bài 4: Bất phương trình bậc hai một ẩn sách CD

Toán 10 Bài 3: Dấu của tam thức bậc hai sách CD

Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng sách CD

Toán 10 Bài 1: Hàm số và đồ thị sách CD

Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn sách CD

Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách CD

Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp sách CD

Toán 10 Bài 1: Mệnh đề toán học sách CD










































