Toán 10 Bài 6: Ba đường conic Toán 10 bài 6 sách Cánh Diều

1 Đánh giá

Lý thuyết Toán 10 CD bài 6

1. Đường Elip
2. Đường Hypebol
3. Đường Parabol
4. Một số ứng dụng thực tiễn của ba đường conic

Toán 10 Bài 6: Ba đường conic giúp học sinh dễ dàng ghi nhớ kiến thức trọng tâm bài học cũng như áp dụng vào giải toán 10 được GiaiToan đăng tải chi tiết trong bài viết dưới đây, mời các bạn tham khảo.

1. Đường Elip

Trong mặt phẳng toạ độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình

$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 với a > b > 0$ . (1)

Ngược lại, mỗi phương trình có dạng (1), với a > b > 0, đều là phương trình của elip có hai tiêu điểm ${F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right)$ , tiêu cự $2c = 2\sqrt {{a^2} - {b^2}}$ và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a.

Phương trình (1) được gọi là phương trình chính tắc của elip tương ứng.

Ví dụ: Cho elip có phương trình chính tắc $\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1$ . Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.

Giải

Ta có: a² = 25, b² = 16. Do đó $c = \sqrt {{a^2} - {b^2}} = 3$ . Vậy elip có hai tiêu điểm là ${F_1}\left( { - 3;0} \right);{F_2}\left( {3;0} \right)$ và tiêu cự là ${F_1}{F_2} = 2c = 6$ . Ta có $a = \sqrt {25} = 5$ , nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a= 10.

2. Đường Hypebol

Cho hai điểm phân biệt có định ${F_1}$ và ${F_2}$ . Đặt ${F_1}{F_2} = 2c$ . Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho $\left| {M{F_1} - M{F_2}} \right| = 2c$ được gọi là đường hypebol (hay hypebol). Hai điểm ${{F_1},{F_2}}$ được gọi là hai tiêu điểm và ${F_1}{F_2} = 2c$ được gọi là tiêu cự của hypebol đó.

Trong mặt phẳng toạ độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình

$\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$ với a,b > 0. (2)

Ngược lại, mỗi phương trình có dạng (2), với a, b >0, đều là phương trình của hypebol có hai tiêu điểm ${F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right)$ , tiêu cự $2c = 2\sqrt {{a^2} + {b^2}}$ và giá trị tuyệt đối của hiệu các khoảng cách từ mối điểm thuộc hypebol đến hai tiêu điểm bằng 2a.

Phương trình (2) được gọi là phương trình chính tắc của hypebol tương ứng.

Ví dụ: Cho hypebol có phương trình chính tắc $\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1$ . Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?

Giải

Ta có ${a^2} = 9,{b^2} = 16$ , nên $c = \sqrt {{a^2} + {b^2}} = 5$ . Vậy hypebol có hai tiêu điểm là ${F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)$ và có tiêu cự 2c = 10. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng $2{\rm{a}} = 2\sqrt 9 = 6$ .

3. Đường Parabol

Cho một điểm F có định và một đường thẳng $\Delta$ cố định không đi qua F. Tập hợp các điểm M cách đều F và $\Delta$ được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, $\Delta$ được gọi là đường chuẩn, khoảng cách từ F đến $\Delta$ được gọi là tham số tiêu của parabol đó.

Xét (P) là một parabol với tiêu điểm F, đường chuẩn $\Delta$ . Gọi H là hình chiếu vuông góc của F trên $\Delta$ . Khi đó, trong hệ trục toạ độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình

${y^2} = 2p{\rm{x}}$ (với p > 0) (3)

Phương trình (3) được gọi là phương trình chính tắc của parabol (P).

Ngược lại, mỗi phương trình dạng (3), với p > 0, là phương trình chính tắc của parabol có tiêu điểm $F\left( {\frac{p}{2};0} \right)$ và đường chuẩn $\Delta :x = - \frac{p}{2}.$

Ví dụ: Cho parabol $(P):{y^2} = x$ .

a) Tìm tiêu điểm F, đường chuẩn $\Delta$ của (P).

b) Tìm những điểm trên (P) có khoảng cách tới F bằng 3.

Giải

a) Ta có 2p = 1 nên $p = \frac{1}{2}$ .

Parabol có tiêu điểm $F\left( {\frac{1}{4};0} \right)$ và đường chuẩn $\Delta :x = - \frac{1}{4}$

b) Điểm $M\left( {{x_0};{y_0}} \right)$ thuộc (P) có khoảng các tới F bằng 3 khi và chỉ khi ${y_0}^2 = {x_0}$ và MF = 3.

Do $MF = d\left( {M,\Delta } \right)$ nên $d\left( {M,\Delta } \right) = 3$

Mặt khác $\Delta :x + \frac{1}{4} = 0 và {x_0} = {y_0}^2 \ge 0 nên 3 = d\left( {M,\Delta } \right) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}.$

Vậy ${x_0} = \frac{{11}}{4} và {y_0} = \frac{{\sqrt {11} }}{2} hoặc {y_0} = - \frac{{\sqrt {11} }}{2}.$

Vậy có hai điểm M thoả mãn bài toán với toạ độ là $\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right)$ và $\left( {\frac{{11}}{4}; - \frac{{\sqrt {11} }}{2}} \right)$ .

4. Một số ứng dụng thực tiễn của ba đường conic

- Ba đường conic có nhiều ứng dụng trong thực tiễn. Ta nêu ra một vài ứng dụng của ba đường conic.

+ Năm 1911, nhà vật lí học người Anh là Ernest Rutherford (1871 - 1937) đã để xuất mô hình hành tỉnh nguyên tử, trong đó hạt nhân nhỏ bé nằm tại tâm của nguyên tử, còn các electron bay quanh hạt nhân trên các quỹ đạo hình elip như các hành tỉnh bay quanh Mặt Trời (Hình sau).

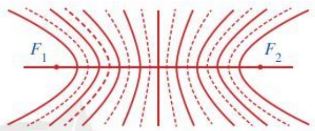
Toán 10 Bài 6: Ba đường conic

+ Trong vật lí, hiện tượng hai sóng gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng giao thoa của hai sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa (Hình sau).

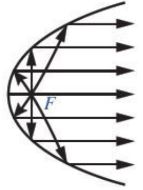
Toán 10 Bài 6: Ba đường conic

+ Với gương parabol, tia sáng phát ra từ tiêu điểm (tia tới) chiếu đến một điểm của parabol sẽ bị hắt lại (ủa phản xạ) theo một tỉa song song (hoặc trùng) với trục của parabol (Hình sau).

Toán 10 Bài 6: Ba đường conic

- Tính chất trên có nhiều ứng dụng, chẳng hạn:

+ Đèn pha: Bề mặt của đèn pha là một mặt tròn xoay sinh bởi một cung parabol quay quanh trục của nó, bóng đèn được đặt ở vị trí tiêu điểm của parabol đó (Hình sau). Các tia sáng phát ra từ bóng đèn khi chiếu đến bề mặt của đèn pha sẽ bị hắt lại theo các tỉa sáng song song, cho phép chúng ta quan sát được các vật ở xa.

Toán 10 Bài 6: Ba đường conic

+ Chảo vệ tinh cũng có dạng như đèn pha. Điểm thu và phát tín hiệu của máy được đặt ở vị trí tiêu điểm của parabol (Hình sau).

Toán 10 Bài 6: Ba đường conic

Trắc nghiệm Toán 10 Bài 6: Ba đường conic

Toán 10 Bài 6: Ba đường conic chương 7 Cánh Diều 10 tập 2 do GiaiToan tổng hợp và đăng tải nhằm giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tại chuyên mục Lý thuyết Toán 10 CD có đầy đủ các các bài học chia theo từng chương bám sát chương trình học SGK Cánh diều 10 đồng thời tại chuyên mục Giải Toán 10 Cánh Diều Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn luyện tại nhà.