Toán 10 Bài 1: Tọa độ của vectơ Toán 10 bài 1 sách Cánh Diều

1 Đánh giá

Lý thuyết Toán 10 CD bài 1

1. Toạ độ của một điểm
2. Toạ độ của một vectơ
3. Liên hệ giữa toạ độ của điểm và toạ độ của vectơ

Toán 10 Bài 1: Tọa độ của vectơ giúp học sinh dễ dàng ghi nhớ kiến thức trọng tâm bài học cũng như áp dụng vào giải toán 10 được GiaiToan đăng tải dưới đây, mời các bạn cùng tham khảo.

1. Toạ độ của một điểm

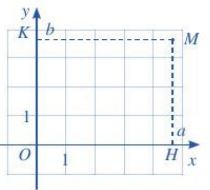
Toán 10 Bài 1: Tọa độ của vectơ

Để xác định toạ độ của một điểm M tuỳ ý trong mặt phẳng toạ độ Oxy, ta làm như sau:

+ Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

+ Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm /M.

Cặp số (a; b) là toạ độ của điểm M trong mặt phẳng toạ độ Oxy. Ta kí hiệu là M(a; b).

2. Toạ độ của một vectơ

Toạ độ của điểm M được gọi là toạ độ của vectơ $\overrightarrow {OM}$ .

Nếu $\overrightarrow {OM}$ có toạ độ (a ; b) thì ta viết $\overrightarrow {OM} = (a; b)$ , trong đó a gọi là hoành độ của vectơ $\overrightarrow {OM}$ và b gọi là tung độ của vectơ $\overrightarrow {OM}$ (Hình sau).

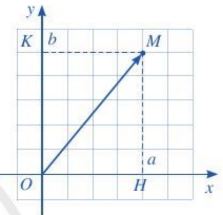
Toán 10 Bài 1: Tọa độ của vectơ

+ Với mỗi vectơ $\overrightarrow u$ trong mặt phẳng toạ độ Oxy, toạ độ của vectơ $\overrightarrow u$ là toạ độ của điểm A sao cho $\overrightarrow {OA} = \overrightarrow u$ .

+ Trong mặt phẳng toạ độ Oxy, nếu $\overrightarrow u = \left( {a;b} \right)$ thì $\overrightarrow u = a\overrightarrow i + b\overrightarrow j$ . Ngược lại, nếu $\overrightarrow u = a\overrightarrow i + b\overrightarrow j$ thì $\overrightarrow u = \left( {a;b} \right)$ .

Chú ý: Với $\overrightarrow a = \left( {{x_1};{y_1}} \right)$ và $\overrightarrow b = \left( {{x_2};{y_2}} \right)$ , ta có:

$\overrightarrow a = \overrightarrow b = \left\{ \begin{array} {l} {x_1} = {x_2}\\ {y_1} = {y_2} \end{array} \right.$

Như vậy, mỗi vectơ hoàn toàn được xác định khi biết toạ độ của nó.

Ví dụ: Trong mặt phẳng toạ độ Oxy, cho điểm A(1; 2) và vectơ $\overrightarrow u$ = (3 ;- 4).

a) Biểu diễn vectơ $\overrightarrow OA$ qua vectơ $\overrightarrow i$ và $\overrightarrow j$ .

b) Biểu diễn vectơ $\overrightarrow u$ qua vectơ $\overrightarrow i$ và $\overrightarrow j$ .

Giải

a) Vì điểm A có toạ độ là (1 ; 2) nên $\overrightarrow OA$ = (1; 2). Do đó:

$\overrightarrow {OA} = 1\overrightarrow i + 2\overrightarrow j = \overrightarrow i + 2\overrightarrow j$ .

b) Vì $\overrightarrow u =(3; - 4)$ nên $\overrightarrow u = 3\overrightarrow i + \left( { - 4} \right)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j$ .

3. Liên hệ giữa toạ độ của điểm và toạ độ của vectơ

Trong mặt phẳng toạ độ Oxy, cho hai điểm $A\left( {{x_A};{y_A}} \right)$ và $B\left( {{x_B};{y_B}} \right)$ .

Ta có: $\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$

Ví dụ: Trong mặt phẳng toạ độ Oxy, cho ba điểm A(1; 1), B(4; 3), C(-1; -2) không thẳng hàng.

a) Tìm toạ độ của vectơ $\overrightarrow {AB}$ .

b) Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Giải

a) Ta có: $\overrightarrow {AB} = \left( {4 - 1;3 - 1} \right)$ . Vậy $\overrightarrow {AB} = \left( {3;2} \right)$ .

b) Gọi toạ độ của điểm D là $\left( {{x_D};{y_D}} \right)$ , ta có: $\overrightarrow {DC} = \left( { - 1 - {x_D}; - 2 - {y_D}} \right)$ .

Tứ giác ABCD là hình bình hành khi và chỉ khi:

$\overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {DC} = \left( {3;2} \right) \Leftrightarrow \left\{ \begin{array}{l} - 1 - {x_D} = 3\\ - 2 - {y_D} = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x_D} = - 4\\ {y_D} = - 4 \end{array} \right.$

Vậy D(- 4;- 4).

Toán 10 Bài 1: Tọa độ của vectơ chương 7 Cánh Diều 10 tập 2 do GiaiToan tổng hợp và đăng tải nhằm giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tại chuyên mục Lý thuyết Toán 10 CD có đầy đủ các các bài học chia theo từng chương bám sát chương trình học SGK Cánh diều 10 đồng thời tại chuyên mục Giải Toán 10 Cánh Diều Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn luyện tại nhà.