Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác sách CD Giải Toán 10 sách Cánh Diều

1 Đánh giá

GiaiToan xin giới thiệu tới các em bài Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác trang 62 sách Cánh Diều. Với phần tóm tắt lý thuyết cùng với bài tập cụ thể giúp các em học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10. Mời các em cùng tham khảo.

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

I. Giá trị lượng giác của một góc từ 0 đến 180
II. Định lí Cosin
III. Định lí Sin
IV. Giải Toán 10 bài 1 SGK + SBT Cánh Diều

I. Giá trị lượng giác của một góc từ 0 đến 180

1. Giá trị lượng giác của một góc từ 0 đến 180

+) Với mỗi góc $\alpha ({0^o} \le \alpha {\rm{\;}} \le {180^o})$ có duy nhất điểm $M({x_0};{y_0})$ trên nửa đường tròn đơn vị để $\widehat {xOM} = \alpha$ .Khi đó:

$\sin \alpha {\rm{\;}} = {y_0}$ là tung độ của M

$\cos \alpha {\rm{\;}} = {x_0}$ là hoành độ của M

$\tan \alpha {\rm{\;}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha {\rm{\;}} \ne {90^o})$

$\cot \alpha {\rm{\;}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha {\rm{\;}} \ne {0^o},\alpha {\rm{\;}} \ne {180^o})$

2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Hai góc bù nhau, $\alpha$ và ${180^o} - \alpha$ :

$\begin{array}{*{20}{l}}{\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha }\\{\cos \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \cos \alpha }\\{\tan \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o})}\\{\cot \left( {{{180}^o} - \alpha } \right) = {\rm{\;}} - \cot \alpha ({0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}$

Hai góc phụ nhau, $\alpha$ và ${90^o} - \alpha$ :

$\begin{array}{*{20}{l}}{\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha }\\{\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha }\\{\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\\{\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}$

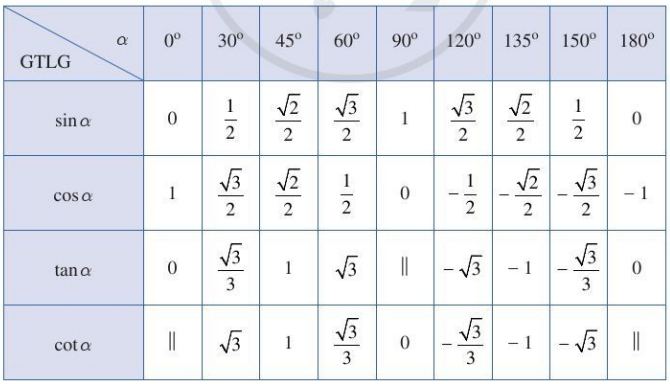
3. Các giá trị lượng giác của một số góc đặc biệt

Các giá trị lượng giác của một số góc đặc biệt

II. Định lí Cosin

1. Định lí cosin

Trong tam giác ABC:

$\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc\cos A}\\{{b^2} = {c^2} + {a^2} - 2ca\cos B}\\{{c^2} = {a^2} + {b^2} - 2ab\cos C}\end{array}$

2. Hệ quả

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$

III. Định lí Sin

1. Định lí sin

Trong tam giác $ABC: \frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.$

(R là bán kính đường tròn ngoại tiếp tam giác ABC)

2. Hệ quả

Hệ quả

$a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C$

$\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.$

IV. Giải Toán 10 bài 1 SGK + SBT Cánh Diều

>>> Bài tiếp theo: Toán 10 Bài 2: Giải tam giác sách CD

>>> Bài trước: Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai sách CD

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác sách CD được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp các em củng cố kiến thức cũng như áp dụng tốt vào giải bài tập Toán lớp 10. Chúc các em học tốt, ngoài ra các em có thể tham khảo thêm các dạng bài tập Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều Tập 1 do GiaiToan biên soạn nhé.