Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng sách CD Giải Toán 10 sách Cánh Diều

1 Đánh giá

Lý thuyết Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng trang 39 sách Cánh Diều được GiaiToan biên soạn và đăng tải. Nội dung của bài bao gồm tóm tắt phần lý thuyết cùng với bài tập cụ thể, giúp các em học sinh nắm chắc kiến thức trọng tâm cũng như nâng cao kỹ năng giải bài tập Toán lớp 10. Mời các em cùng tham khảo.

Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

I. Hàm số bậc hai
II. Đồ thị hàm số bậc hai
III. Ứng dụng
IV. Giải Toán 10 bài 2 SGK + SBT Cánh Diều

I. Hàm số bậc hai

+ Định nghĩa:

Hàm số bậc hai là hàm số cho bằng công thức dạng $y = a{x^2} + bx + c$ với $a,b,c \in \mathbb{R};a \ne 0.$

+ Tập xác định: $\mathbb{R}$

II. Đồ thị hàm số bậc hai

+) Đồ thị hàm số bậc hai $y = f(x) = a{x^2} + bx + c (a \ne 0)$ là một parabol (P):

- Đỉnh $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$

- Trục đối xứng: đường thẳng $x = - \frac{b}{{2a}}$

- Bề lõm: quay lên trên nếu a > 0, quay xuống dưới nếu a < 0

- Cắt Oy tại điểm (0;c)

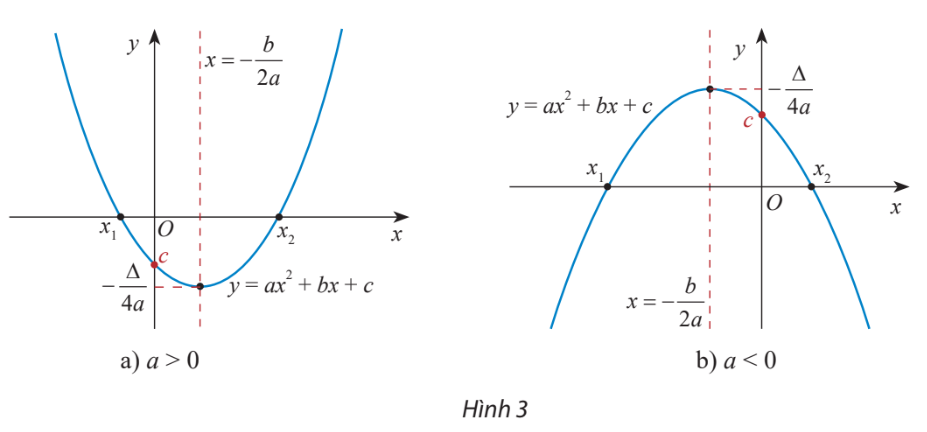
Đồ thị hàm số bậc hai

* Chú ý: Nếu PT $a{x^2} + bx + c = 0$ có hai nghiệm ${x_1},{x_2}$ thì đồ thị hàm số $y = a{x^2} + bx + c$ cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.

+) Vẽ đồ thị

1) Xác định đỉnh $S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)$

2) Vẽ trục đối xứng $d: x = - \frac{b}{{2a}}$

3) Tìm tọa độ giao điểm của đồ thị với trục tung $(A(0;c))$ , trục hoành (nếu có).

Xác định $B\left( {\frac{{ - b}}{a};c} \right)$ (là điểm đối xứng với A qua d)

4) Vẽ parabol đỉnh S, trục đối xứng d, đi qua các điểm tìm được.

III. Ứng dụng

+) Bảng biến thiên

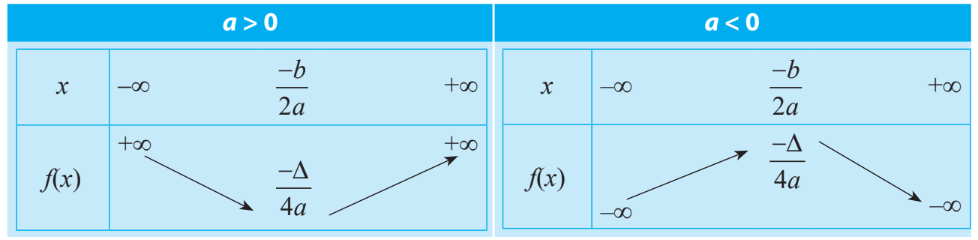
Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

+) Ứng dụng của hàm số bậc hai

IV. Giải Toán 10 bài 2 SGK + SBT Cánh Diều

>>> Bài tiếp theo: Toán 10 Bài 3: Dấu của tam thức bậc hai sách CD

>>> Bài trước: Toán 10 Bài 1: Hàm số và đồ thị sách CD

GiaiToan đã chia sẻ xong bài Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng sách CD. Hy vọng với tài liệu này sẽ giúp ích cho các em nắm được trọng tâm của bài, từ đó áp dụng vào giải các bài tập về Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng. Qua đó chuẩn bị cho bài thi giữa học kì và cuối học kì môn Toán lớp 10. Ngoài tham khảo tài liệu trên, các em cũng đừng quên tham khảo thêm các dạng bài tập Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều Tập 1 do GiaiToan biên soạn nhé. Chúc các em học tốt.