Toán 10 Bài 2: Giải tam giác sách CD Giải Toán 10 sách Cánh Diều

1 Đánh giá

Lý thuyết Giải tam giác. Tính diện tích tam giác trang 72 sách Cánh Diều được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm lí thuyết cùng với bài tập cụ thể, giúp các em ôn tập, rèn luyện giải bài tập Toán lớp 10. Mời các em cùng tham khảo.

Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác

1. Lý thuyết Giải tam giác. Tính diện tích tam giác
2. Tính diện tích tam giác
3. Áp dụng vào bài toán thực tiễn

1. Lý thuyết Giải tam giác. Tính diện tích tam giác

Giải tam giác

Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:

– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;

– Biết độ dài ba cạnh;

– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

Ví dụ: Cho tam giác ABC có $A B=4, B C=6, A C=2 \sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB.

a) Tính cos các góc của tam giác ABC.

b) Tính độ dài cạnh AM.

Hướng dẫn giải:

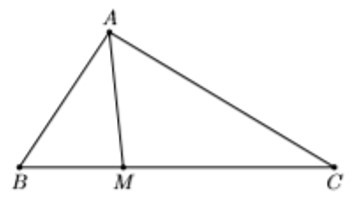
Lý thuyết Giải tam giác. Tính diện tích tam giác

a) Theo định lí cosin trong tam giác ABC ta có:

$\begin{aligned} &\cos B=\frac{A B^2+B C^2-A C^2}{2 A B \cdot B C}=\frac{4^2+6^2-(2 \sqrt{7})^2}{2 \cdot 4 \cdot 6}=\frac{1}{2}\\ &\Rightarrow \widehat{B}=60^{\circ} \text {. }\\ &\cos \mathrm{C}=\frac{\mathrm{AC}^2+\mathrm{BC}^2-\mathrm{AB}^2}{2 \mathrm{AC} \cdot \mathrm{BC}}=\frac{(2 \sqrt{7})^2+6^2-4^2}{2.2 \sqrt{7} .6}=\frac{2 \sqrt{7}}{7} \end{aligned}$

b) Ta có:

$\begin{aligned} &\mathrm{MC}=2 \mathrm{MB} \Rightarrow \frac{\mathrm{MB}}{\mathrm{MC}}=\frac{1}{2} \Rightarrow \frac{\mathrm{MB}}{\mathrm{BC}}=\frac{1}{3} \\ &\Rightarrow \mathrm{MB}=\frac{1}{3} \mathrm{BC}=\frac{1}{3} \cdot 6=2 \end{aligned}$

Áp dụng định lí côsin trong tam giác AMB ta có:

$\begin{aligned} &\mathrm{AM}^2=\mathrm{AB}^2+\mathrm{BM}^2-2 \mathrm{AB} \cdot \mathrm{BM} \cdot \cos \mathrm{B}=4^2+2^2-2 \cdot 4 \cdot 2 \cdot \frac{1}{2}=12 \\ &\Rightarrow \mathrm{AM}=\sqrt{12}=2 \sqrt{3} \end{aligned}$

Ví dụ: Cho tam giác ABC có $\widehat{B}=35^{\circ} ; \widehat{C}=50^{\circ}$ và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).

Hướng dẫn giải:

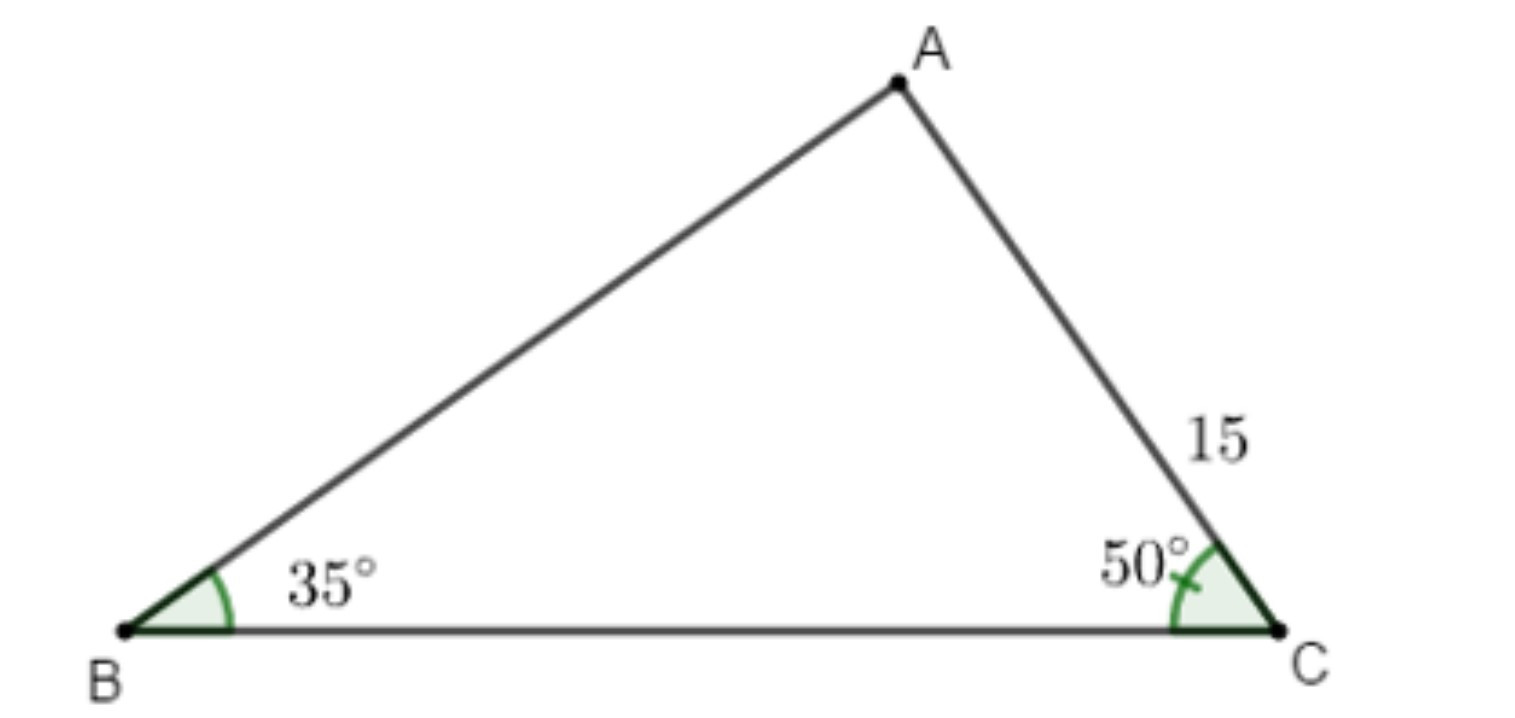
Ta có:

$\widehat{\mathrm{A}}+\widehat{\mathrm{B}}+\widehat{\mathrm{C}}=180^{\circ}$ (tổng ba góc trong tam giác)

Suy ra:

$\widehat{\mathrm{A}}=180^{\circ}-\widehat{\mathrm{B}}-\widehat{\mathrm{C}}=180^{\circ}-35^{\circ}-50^{\circ}=95^{\circ}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{B C}{\sin A}=\frac{A C}{\sin B}=\frac{A B}{\sin C}$

Suy ra:

$\begin{aligned} &\mathrm{BC}=\frac{\mathrm{AC} \cdot \sin \mathrm{A}}{\sin B}=\frac{15 \cdot \sin 95^{\circ}}{\sin 35^{\circ}} \approx 26,05 \mathrm{~cm} \\ &\mathrm{AB}=\frac{\mathrm{AC} \cdot \sin C}{\sin B}=\frac{15 \cdot \sin 50^{\circ}}{\sin 35^{\circ}} \approx 20,03 \mathrm{~cm} \end{aligned}$

Vậy BC = 26,05cm và AB ≈ 20,03 cm.

2. Tính diện tích tam giác

Công thức tính diện tích tam giác:

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

$S=\frac{1}{2} b c \cdot \sin A=\frac{1}{2} c a \cdot \sin =\frac{1}{2} a b \cdot \sin C$

Ví dụ: Cho tam giác ABC có $BC=4\sqrt{2}, \widehat{\mathrm{A}}=45^{o}, \widehat{\mathrm{B}}=120^{o}$ . Tính diện tích tam giác ABC.

Hướng dẫn giải:

Ta có:

$\widehat{\mathrm{A}}+ \widehat{\mathrm{B}}+\widehat{\mathrm{C}}=180^{o}$ (tổng ba góc trong tam giác)

Suy ra: $\widehat{\mathrm{C}}=180^{o} -\widehat{\mathrm{A}}-\widehat{\mathrm{B}}=180^{o} -45^{o} -120^{o} =15^{o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{B C}{\sin A}=\frac{A C}{\sin B}=\frac{A B}{\sin C}$

Suy ra:

$AC=\frac{B C.sinB}{\sin A}= \frac{4\sqrt2{}.sin120^{o} }{\sin 45^{o} }=4\sqrt{3};$

$AC=\frac{A C.sinC}{\sin B}= \frac{4\sqrt3{}.sin15^{o} }{\sin 12^{o} }=2\sqrt{6}-2\sqrt{2} ;$

Diện tích tam giác ABC là:

$S=\frac{1}{2}AC.AB.\sin A=\frac{1}{2}.4\sqrt{3}.\left(2\sqrt{6}-2\sqrt{2}\right).\sin45^o=12-4\sqrt{3}$ (đơn vị diện tích).

Công thức Heron:

Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $p=\frac{a+b+c}{2}.$ . Khi đó, diện tích S của tam giác ABC là:

$S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$

Trong đó p là nửa chu vi tam giác ABC.

Ví dụ: Chứng minh công thức Heron.

Chứng minh công thức Heron

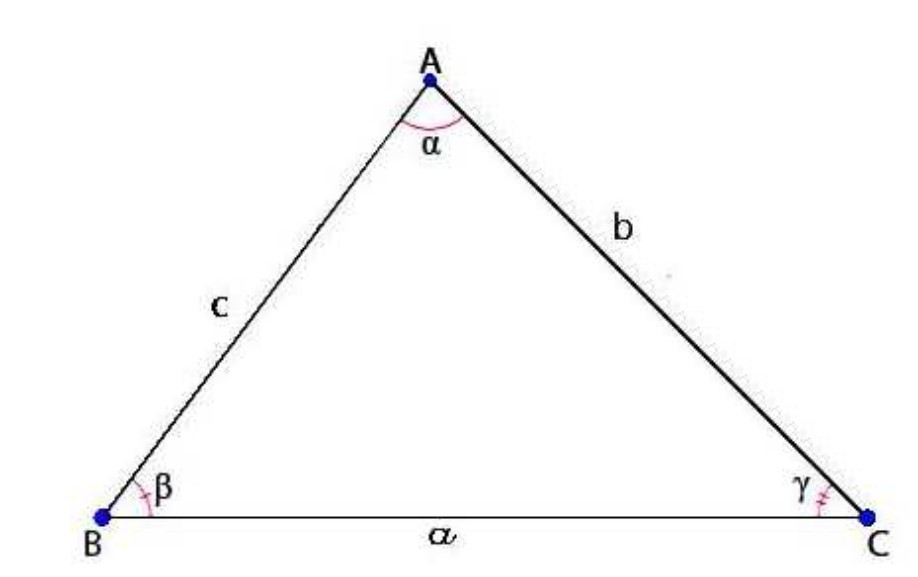
Hướng dẫn giải:

Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:

$\cos C=\frac{a^2+b^2+c^2}{2ab}$

Mà:

sin²C + cos²C = 1

$=>\sin\ C=\sqrt{1-\cos^2C}=\sqrt{1-\left(\frac{a^2+b^2+c^2}{2ab}\right)}=\frac{\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^2}}{2ab}$

Ta có công thức tính diện tích tam giác ABC:

$S=\frac{1}{2}ab\sin C$

$=\frac{1}{2}ab.\frac{\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^{2} }}{2ab}$

$=\frac{1}{4} {\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^{2} }}$

$=\frac{1}{4}\sqrt{\left(2ab-\left(a^2+b^2-c^2\right)\right)\left(2ab+\left(a^2+b^2-c^2\right)\right)}$

$=\frac{1}{4}\sqrt{\left(c^2-\left(a-b\right)^2\right)\left(\left(a+b\right)^2-c^2\right)}$

$=\frac{1}{4}\sqrt{\left(c\left(a-b\right)\right)\left(c+\left(a-b\right)\right)\left(\left(a+b\right)-c\right)\left(\left(a+b\right)+c\right)}$

$=\frac{1}{4}\sqrt{\left(a+b+c\right)\left(c-a+b\right)\left(c+a-b\right)\left(a+b-c\right)}$

$\frac{1}{2}\left(a+b+c\right).\frac{1}{2}\left(a+b+c-2a\right).\frac{1}{2}\left(a+b+c-2b\right).\frac{1}{2}\left(a+b+c-2c\right)$

$=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$

Với $p=\frac{a+b+c}{2}$

Suy ra $S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$ (đpcm).

Ví dụ: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Nửa chu vi tam giác ABC là:

$p=\frac{AB+AC+BC}{2}=\frac{5+6+9}{2}=10$

Áp dụng công thức Heron, diện tích tam giác ABC là:

$S=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}=\sqrt{10\left(10-5\right)\left(10-6\right)\left(10-9\right)}=10\sqrt{2}$ (đvdt)

3. Áp dụng vào bài toán thực tiễn

Trong thực tiễn, ta có thể áp dụng hệ thức lượng trong tam giác vào các bài toán như tính khoảng cách giữa hai vị trí, tính diện tích,... giúp cho việc tính toán trở nên chính xác và nhanh chóng hơn. Chúng ta có thể xem ví dụ sau:

Ví dụ: Đường dây cao thế nối thẳng từ vị trí A đến vị trí B dài 10 km, từ vị trí A đến vị trí C dài 8 km, góc tạo bởi hai đường dây trên bằng 75°. Tính khoảng cách từ vị trí B đến vị trí C (làm tròn đến chữ số thập phân thứ 2).

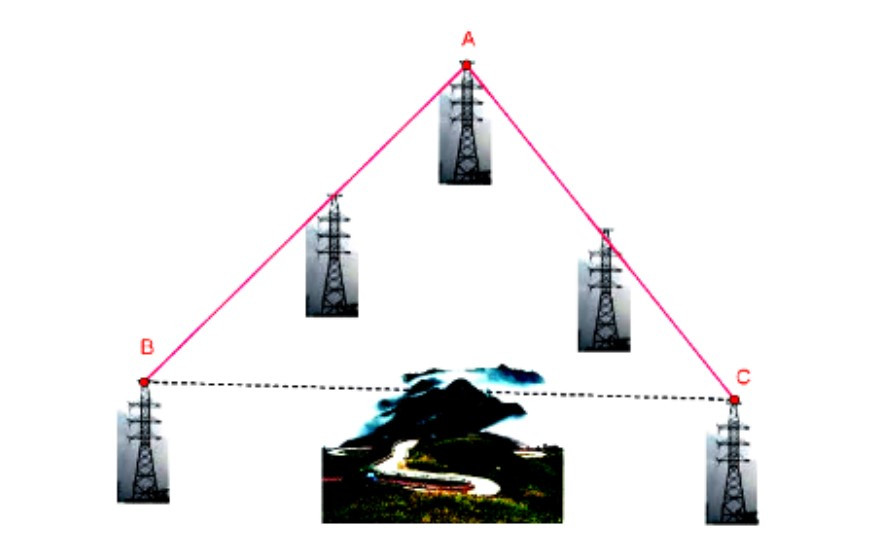
Toán 10 Bài 2: Giải tam giác sách CD

Hướng dẫn giải:

Áp dụng định lí cosin vào tam giác ABC ta có:

$BC^2=AB^2+AC^2-2AB.AC.\cos A=8^2+10^2-2.8.10.\cos75^o \approx 122,59$

$BC\approx11,07$

Vậy khoảng cách từ B đến C là khoảng 11,07 km.

4. Giải Toán 10 bài 2 SGK + SBT Cánh Diều

>>> Bài tiếp theo: Toán 10 Bài 3: Khái niệm vectơ sách CD

>>> Bài trước: Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác sách CD

Toán 10 Bài 2: Giải tam giác sách CD được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, củng cố kiến thức cũng như áp dụng giải các bài tập về Giải tam giác. Tính diện tích tam giác từ đó chuẩn bị tốt cho bài thi giữa học kì và cuối kì môn Toán lớp 10. Chúc các em học tốt, ngoài ra các em cũng có thể tham khảo thêm các dạng bài tập Toán lớp 10 tại chuyên mục Giải Toán 10 Cánh Diều Tập 1 do GiaiToan biên soạn nhé.