Toán 7 Bài tập cuối chương 8 Toán 7 sách Chân trời sáng tạo

1 Đánh giá

Lý thuyết Bài tập cuối chương 8 - Toán lớp 7 Chân trời sáng tạo trang 84 SGK được GiaiToan biên soạn và đăng tải, thông qua bài giảng này các em dễ dàng hệ thống lại toàn bộ kiến thức đã học, bên cạnh đó các em còn nắm được phương pháp giải các bài tập và vận dụng vào giải các bài tập tương tự. Chúc các em học tốt, mời các em tham khảo nội dung bài chi tiết dưới đây.

1. Tóm tắt lý thuyết

1.1. Góc và cạnh của một tam giác

a) Tổng số đa ba góc của một tam giác

Tổng số đo ba góc của một tam giác bằng 180 0

Chú ý:

- Tam giác có 3 góc nhọn được gọi là tam giác nhọn.

- Tam giác có 1 góc vuông được gọi là tam giác vuông, cạnh đôi điện góc vuông gọi là canh huyền, hai cạnh còn lại gọi là hai cạnh góc vuông.

- Tam giác có 1 góc tù được gọi là tam giác tù.

b) Quan hệ giữa ba cạnh của một tam giác

Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

Nhận xét: Trong một tam giác, độ đài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ đài của hai cạnh còn lại

Lưu ý: Khi xét độ dài ba đoạn thẳng có thoả mãn các bắt đẳng thức tam giác hay không, ta chỉ cân so sánh độ đài lớn nhật với tông của hai đô đài còn lại, hoặc so sánh độ đài nhỏ nhât với hiệu của hai độ dài còn lại.

1.2. Tam giác bằng nhau - Tam giác cân

a) Tam giác bằng nhau

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Chú ý: Khi vẽ hình hai tam giác bằng nhau, các cạnh hoặc các góc bằng nhau được đánh dấu bởi những kí hiệu giỗng nhau (Hình bên dưới)

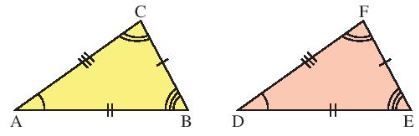
- Trường hợp bằng nhau thứ nhất: Cạnh - cạnh - cạnh (c.c.c): Nếu ba cạnh của lam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

- Trường hợp bằng nhau thứ hai: Cạnh - góc - cạnh (c.g.c): Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

- Trường hợp bằng nhau thứ ba: góc - cạnh - góc (g.c.g): Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đỏ bằng nhau.

b) Tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau.

Tam giác ABC với AB = AC (Hình bên dưới) được gọi là tam giác cân tại A, AB, AC là các cạnh bên, BC là cạnh đáy, $\widehat B$ và $\widehat C$ là các góc ở đáy, $\widehat A$ là góc ở đình.

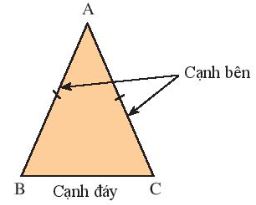
+ Định lí 1: Trong một tam giác cân hai góc ở đáy bảng nhau.

+ Định lí 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

1.3. Đường vuông góc và đường xiên

a) Quan hệ giữa cạnh và góc trong một tam giác

Trong một tam giác, đố diện với góc lớn hơn là cạnh lớn hơn và ngược lại, đối điện với cạnh lớn hơn là góc lớn hơn.

b) Đường vuông góc và đường xiên

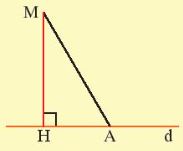
- Đoạn tháng MH gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm M đến đường thẳng d.

- Đoạn thẳng MA gọi là một đường xiên kẻ từ điểm M đến đường thẳng d.

- Độ dài đoạn MH được gọi là khoảng cách từ điểm M đền đường thẳng d.

c) Mối quan hệ giữa đường vuông góc và đường xiên

Trong số các đoạn thẳng nối từ một điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.

1.4. Đường trung trực của một đoạn thẳng

Đường thắng vuông góc với một đoạn thắng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.

Định lí 1: Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Định lí 2: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

1.5. Tính chất ba đường trung trực, ba đường trung tuyến

a) Tính chất ba đường trung trực của tam giác

Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.

Định lí: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

b) Tính chất ba đường trung tuyến của tam giác

Đường trung tuyến của tam giác là đoạn thằng nối một đỉnh của tam giác với trung điểm cạnh đối diện.

Định lí: Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ đài đường trung tuyến đi qua đỉnh ấy.

1.6. Tính chất ba đường đường cao, ba đường phân giác

c) Tính chất ba đường cao của tam giác

Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thắng chứa cạnh đổi điện gọi là đường cao của tam giác đó.

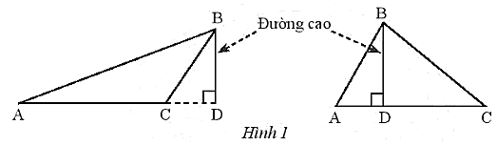
Định lí: Ba đường cao của một tam giác cùng đi qua một điểm.

d) Tính chất ba đường phân giác của tam giác

Cho tam giác ABC, tia phân giác của góc A cắt cạnh BC tại D. Khi đó đoạn thẳng AD được gọi là đường phân giác (của góc A) của tam giác ABC.

Ba đường phân giác của một tam giác củng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác.

2. Bài tập minh họa

Câu 1: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?

a) 7cm; 8cm; 11cm

b) 7cm; 9cm; 16cm

c) 8cm; 9cm; 16cm

Hướng dẫn giải

a) Vì 7 + 8 > 11

Nên a là một tam giác theo bất đẳng thức tam giác

b) Vì 7 + 9 = 16 không thỏa mãn bất đẳng thức tam giác nên b không phải là tam giác

c) Vì 8 + 9 > 16

Nên c là một tam giác theo bất đẳng thức tam giác

Câu 2: Tìm các tam giác cân trong hình sau và đánh dấu vào các cạnh bằng nhau.

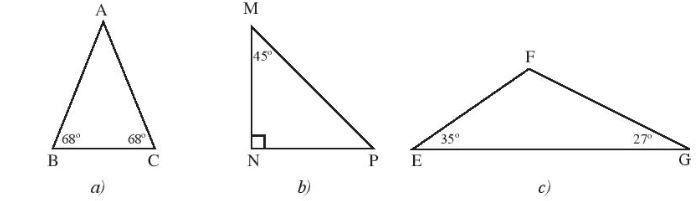
Hướng dẫn giải

a) Ta có tam giác ABC cân tại A do 2 góc đáy B, C cùng bằng 68°

Nên AB = AC

b) Vì tổng các góc trong tam giác = 180° nên $\widehat M + \widehat N + \widehat P = {180^o}$

$\Rightarrow \widehat P = {180^o} - {45^o} - {90^o} = {45^o}$

$\Rightarrow \Delta MNP$ vuông cân tại N

$\Rightarrow MN = NP$

c) Xét $\Delta EFG$ theo định lí về tổng số đo các góc trong tam giác ta có:

$\Rightarrow \widehat F + \widehat E + \widehat G = {180^o}$

$\Rightarrow \widehat F = {180^o} - {35^o} - {27^o} = {118^o}$

$\Rightarrow \Delta EFG$ không cân nên không có các cặp cạnh bằng nhau

Câu 3: Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC.

Hướng dẫn giải

Qua M vẽ đường thẳng vuông góc với BC.

Qua N vẽ đường thẳng vuông góc với CA.

Qua P vẽ đường thẳng vuông góc với AB.

Khi đó ta thu được ba đường trung trực của tam giác ABC.

Ta có hình vẽ sau:

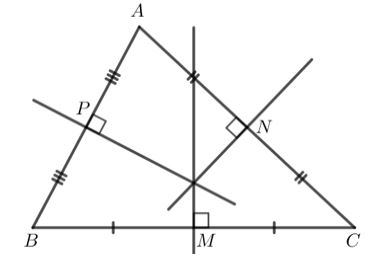
Câu 4: Trong hình sau, G là trọng tâm của tam giác AEF với đường trung tuyến AM.

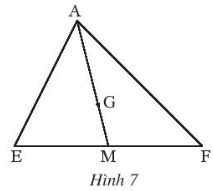
Hãy tính các tỉ số:

$a)\ \dfrac{{GM}}{{AM}}$

$b)\ \dfrac{{GM}}{{AG}}$

$c)\ \dfrac{{AG}}{{GM}}$

Hướng dẫn giải

a) Vì G là trọng tâm của tam giác AEF với đường trung tuyến AM nên theo định lí 3 đường trung tuyến cắt nhau tại trọng tâm ta có :

$\dfrac{{AG}}{{AM}} = \dfrac{2}{3} \Rightarrow \dfrac{{GM}}{{AM}} = 1 - \dfrac{2}{3} = \dfrac{1}{3}$

b) Vì $\dfrac{{AG}}{{AM}} = \dfrac{2}{3}$ và $\dfrac{{GM}}{{AM}} = \dfrac{1}{3}$ (theo câu a)

$\Rightarrow \dfrac{{GM}}{{AG}} = \dfrac{1}{2}$

c) Vì $\dfrac{{GM}}{{AG}} = \dfrac{1}{2}$ (chứng minh b)

$\Rightarrow \dfrac{{AG}}{{GM}} = 2$

>>> Bài tiếp theo: Toán 7 Bài 1: Làm quen với biến cố ngẫu nhiên

>>> Bài trước: Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác

Toán 7 Bài tập cuối chương 8 được GiaiToan chia sẻ trên đây. Hy vọng thông qua bài giảng này sẽ giúp ích cho các em ôn tập và hệ thống lại các kiến thức trọng tâm của chương, từ đó áp dụng các kiến thức đã học vào giải các bài tập một cách dễ dàng. Ngoài việc tham khảo bài giảng trên các em cũng đừng quên giải các bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 2 CTST do GiaiToan biên soạn để ôn tập nhé.