Toán 7 Bài 1: Góc và cạnh của một tam giác Toán 7 sách Chân trời sáng tạo

Ví dụ: Tìm số đo các góc chưa biết của tam giác trong hình sau:

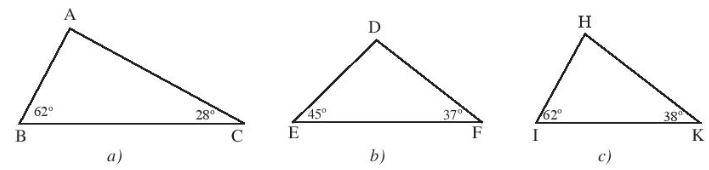
Giải

Áp đụng định lí về tông số đo ba góc của tam giác, ta có:

Chú ý:

- Tam giác có 3 góc nhọn được gọi là tam giác nhọn.

- Tam giác có 1 góc vuông được gọi là tam giác vuông, cạnh đôi điện góc vuông gọi là canh huyền, hai cạnh còn lại gọi là hai cạnh góc vuông.

- Tam giác có 1 góc tù được gọi là tam giác tù.

Xét một tam giác ABC bât kì, ta luôn có các bât đẳng thức sau:

AB + AC > BC;

AB + BC > AC;

AC +BC > AB.

Các bất đẳng thức trên được gọi là bất đẳng thức tam giác.

Từ bât đẳng thức tam giác AB + BC > AC, người ta suy ra:

AB > AC - BC;

BC > AC - AB.

Nhận xét: Trong một tam giác, độ đài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ đài của hai cạnh còn lại

Chẳng hạn, trong tam giác ABC, với cạnh AB, ta có:

AC - BC < AB < AC + BC hay BC - AC < AB < AC + BC.

Ví dụ: Trong các bộ ba độ đài đoạn thẳng dưới đây, bộ ba nào có thể là độ đài ba cạnh của một tam giác?

a) 2 cm; 3 cm; 6 cm;

b) 2 cm; 4 cm; 6 cm;

c) 3 cm; 4 cm; 6 cm

Giải

Ta có:

a) 6 > 2+3;

b) 6 = 2+4;

c) 4 - 3 < 6 < 4 + 3

Vậy chỉ có bộ ba 3 cm; 4 cm; 6 cm có thể là độ dài ba canh của một tam giác.

Lưu ý: Khi xét độ dài ba đoạn thẳng có thoả mãn các bắt đẳng thức tam giác hay không, ta chỉ cân so sánh độ đài lớn nhật với tông của hai đô đài còn lại, hoặc so sánh độ đài nhỏ nhât với hiệu của hai độ dài còn lại.

Câu 1: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?

a) 7cm; 8cm; 11cm

b) 7cm; 9cm; 16cm

c) 8cm; 9cm; 16cm

Hướng dẫn giải

a) Vì 7 + 8 > 11

Nên a là một tam giác theo bất đẳng thức tam giác

b) Vì 7 + 9 = 16 không thỏa mãn bất đẳng thức tam giác nên b không phải là tam giác

c) Vì 8 + 9 > 16

Nên c là một tam giác theo bất đẳng thức tam giác

Câu 2: Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5cm AC = 3cm thì cạnh BC có thể có độ dài là bao nhiêu xăngtimét?

Hướng dẫn giải

Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:

5 - 3 < BC < 5 + 3

2 < BC < 8

Mà BC là số nguyên

Vậy độ dài BC có thể là 3 cm, 4 cm, 5 cm, 6 cm hoặc 7 cm.