Toán 7 Bài 8: Tính chất ba đường cao của tam giác Toán 7 sách Chân trời sáng tạo

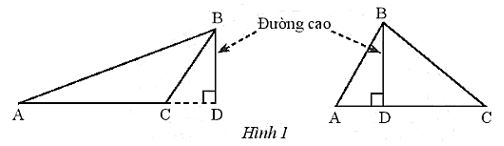
Ví dụ: Trong Hình 1, đoạn thẳng BD là đường cao của tam giác ABC.

Đôi khi ta còn nói đường thẳng BD là đường cao của tam giác ABC.

Chú ý: Mỗi tam giác có ba đường cao.

Định lí:

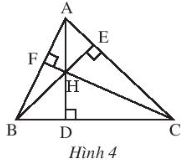
Ví dụ: Trong Hình 4, ba đường cao AD, BE, CF của tam giác ABC cùng đi qua điểm H

Chú ý:

- Ta còn nói ba đường cao AD, BE, CF đồng quy tại H. Điểm H được gọi là trực tâm của tam giác ABC.

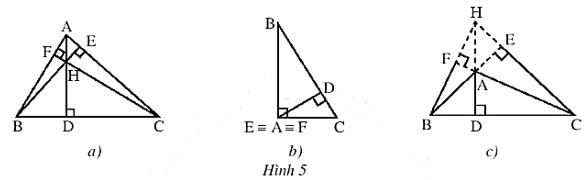
- Tam giác nhọn có trực tâm nằm bên trong tam giác (Hình 5a)

- Tam giác vuông có trực tâm trùng với đỉnh góc vuông (Hình ŠSb)

- Tam giác tù có trực tâm nằm ngoài tam giác (Hình 5c).

Câu 1: Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC

Hướng dẫn giải

Để vẽ đường cao AH của tam giác nhọn ABC ta làm như sau:

Bước 1. Vẽ tam giác nhọn ABC.

Bước 2. Đặt êke sao cho 1 cạnh của êke trùng với cạnh BC, cạnh còn lại đi qua đỉnh A.

Khi đó kẻ 1 đường thẳng từ A đến BC thông qua cạnh đi đỉnh A vừa đặt, ta thu được đường cao đi qua đỉnh A. Đường thẳng này cắt cạnh BC tại một điểm, điểm này chính là điểm H.

Thực hiện tương tự đối với các đường cao BK và CE ta thu được hình vẽ sau:

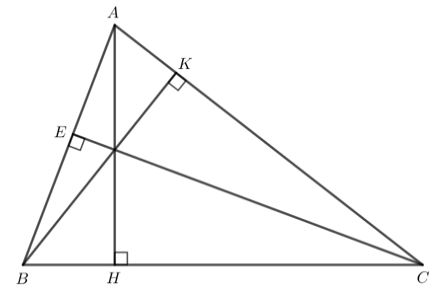
Câu 2: Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.

Hướng dẫn giải

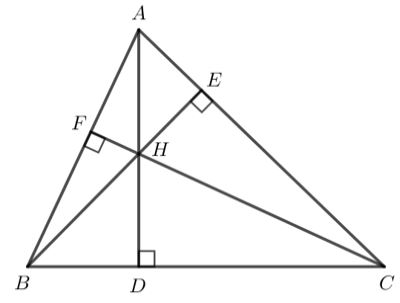
+) Xét tam giác HBC ta có :

HD vuông góc với  là đường cao tam giác HBC

BF vuông góc với HC tại F (kéo dài HC)  là đường cao của tam giác HBC

CE vuông góc với HB tại E (kéo dài HB)  là đường cao của tam giác HBC

Ta kéo dài HD, BF, CE sẽ cắt nhau tại A

là trực tâm tam giác HBC

+) Xét tam giác HAB ta có :

HF vuông góc với  là đường cao tam giác HAB

BH vuông góc với AE tại E (kéo dài HB)  là đường cao của tam giác HAB

BD vuông góc với AH tại D (kéo dài AH)  là đường cao của tam giác HAB

Ta kéo dài HF, BD, AE sẽ cắt nhau tại C

là trực tâm tam giác HAB

+) Xét tam giác HAC ta có :

HE vuông góc với  là đường cao tam giác HAC

AF vuông góc với HC tại F (kéo dài HC)  là đường cao của tam giác HAC

CD vuông góc với AH tại D (kéo dài AH)  là đường cao của tam giác HAC

Ta kéo dài CD, HE, AF sẽ cắt nhau tại B

là trực tâm tam giác HAC.