Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến Toán 7 sách Chân trời sáng tạo

1 Đánh giá

Lý thuyết bài 4: Phép nhân và phép chia đa thức một biến - Toán lớp 7 Chân trời sáng tạo trang 37 SGK được GiaiToan biên soạn và đăng tải. Bài học hôm nay bao gồm các kiến thức được trình bày cụ thể và chi tiết, cùng với các dạng bài tập minh họa giúp các em dễ dàng nắm vững được trọng tâm bài học. Mời các em cùng tham khảo.

Lý thuyết Toán 7 bài 4: Phép nhân và phép chia đa thức một biến

1. Tóm tắt lý thuyết
2. Bài tập minh họa

1. Tóm tắt lý thuyết

1.1. Phép nhân hai đa thức một biến

Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

Ví dụ: Thực hiện phép nhân.

$\begin{array}{l} a)\;\;3x.\left( {2{x^2} - 4x + 5} \right);\\ b)\;\;\left( {2x + 3} \right).\left( {x + 1} \right). \end{array}$

Giải

a) Ta có: $3x.\left( {2{x^2} - 4x + 5} \right) = 3x.\left( {2{x^2}} \right) + 3x.\left( { - 4x} \right) + 3x.5 = 6{x^3} - 12{x^2} + 15..$

Ta nói đa thức $6{x^3} - 12{x^2} + 15$ là tích của 3x và $\left( {2{x^2} - 4x + 5} \right)$

b) Ta có:

$\begin{array}{l} \left( {2x + 3} \right).\left( {x + 1} \right). = 2x.\left( {x + 1} \right) + 3.\left( {x + 1} \right) = 2{x^2} + 2x + 3x + 3\\ = 2{x^2} + 5x + 3 \end{array}$

Ta cũng có thẻ thực hiện phép nhân đa thức theo cách sau:

1.2. Phép chia hai đa thức một biến

*Chia đa thức cho đa thức (chia hết)

Cho hai đa thức P và Q (với $Q \ne 0$ ). Ta nói đa thức P chia hết cho đa thức Q nếu có đa thức M sao cho P = Q . M

TTa gọi P là đa thức bị chia, Q là đa thức chia và M là đa thức thương (gọi tắt là thương).

Kí hiệu M = P : Q hoặc $M = \frac{P}{Q}.$

Ví dụ: Muốn chia đa thức 3x⁶ - 5x⁵ + 7x⁴ cho 2x³ ta thực hiện như sau:

$\begin{array}{l} \left( {3{x^6}\; - {\rm{ }}5{x^5}\; + {\rm{ }}7{x^4}} \right):2{x^3} = \left( {3{x^6}:2{x^3}} \right) + \left( { - {\rm{ }}5{x^5}:2{x^3}} \right) + \left( {7{x^4}:2{x^3}} \right)\\ = \frac{3}{2}{x^3} - \frac{5}{2}{x^2} + \frac{7}{2}x \end{array}$

*Chia đa thức cho đa thức (chia có dư)

Ví dụ: Đề thực hiện phép chia đa thức $P\left( x \right) = 3{x^2} - 5x + 2$ cho $Q\left( x \right) = x - 2$ thì ta làm tương tự như trên và có:

Phép chia nêu trên có dư là 4 và ta có: $3{x^2} - 5x + 2 = \left( {x - 2} \right)\left( {3x + 1} \right) + 4.$

Nhận xét: Khi chia đa thức A cho đa thức B với thương là Q, dư là R thì A = B.Q + R, trong đó bậc của R nhỏ hơn bậc của B.

1.3. Tính chất của phép nhân đa thức một biến

Cho A, B, C là các đa thức một biến với cùng một biến số. Ta có:

* A . B = B . A;

* A . (B . C) = (A . B) . C.

Ví dụ: Thực hiện phép tính: $6.\left( {{x^2} - 2} \right).\frac{1}{2}.$

Giải

$\begin{array}{l} 6.\left( {{x^2} - 2} \right).\frac{1}{2} = 6.\left[ {\left( {{x^2} - 2} \right).\frac{1}{2}} \right] = 6.\left[ {\frac{1}{2}.\left( {{x^2} - 2} \right)} \right]\\ = \left( {6.\frac{1}{2}} \right).\left( {{x^2} - 2} \right) = 3.\left( {{x^2} - 2} \right) = 3{x^2} - 6 \end{array}$

2. Bài tập minh họa

Câu 1: Thực hiện phép nhân $(4x - 3)(2{x^2} + 5x - 6)$

Hướng dẫn giải

$\begin{array}{l}(4x - 3)(2{x^2} + 5x - 6)\\ = 4x.2{x^2} + 4x.5x - 6.4x - 3.2{x^2} - 3.5x + 18\\ = 8{x^3} + 20{x^2} - 6{x^2} - 24x - 15x + 18\\ = 8{x^3} + 14{x^2} - 39x + 18\end{array}$

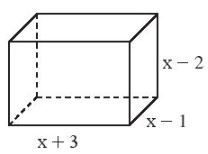
Câu 2: Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.

Hướng dẫn giải

Thể tích hình hộp chữ nhật là:

$\begin{array}{l}(x + 3).(x - 1).(x - 2)\\ = \left[ {(x + 3).(x - 1)} \right].(x - 2)\\ = (x.x - 1.x + 3.x - 3.1)(x - 2)\\ = ({x^2} + 2x - 3)(x - 2)\\ = {x^2}.x - 2.{x^2} + 2x.x - 2x.2 - 3.x + 3.2\\ = {x^3} - 7x + 6\end{array}$

Câu 3: Thực hiện các phép chia sau $\frac{{9{x^2} + 5x + x}}{{3x}}$ và $\frac{{(2{x^2} - 4x) + (x - 2)}}{{2 - x}}$

Hướng dẫn giải

$\frac{{9{x^2} + 5x + x}}{{3x}} = \frac{{9{x^2} + 6x}}{{3x}} = \frac{{9{x^2}}}{{3x}} + \frac{{6x}}{{3x}} = 3x + 2$

$\frac{{2{x^2} - 3x - 2}}{{2 - x}} = \frac{{2{x^2} - 3x - 2}}{{ - x + 2}} = - 2x - 1$

>>> Bài tiếp theo: Toán 7 Bài 1: Góc và cạnh của một tam giác

>>> Bài trước: Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến

Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến được GiaiToan chia sẻ trên đây. Hy vọng với bài giảng này sẽ giúp các em thực hiện được phép nhân và phép chia các đa thức một biến, từ đó vận dụng được những tính chất của phép nhân đa thức một biến trong tính toán. Chúc các em học tốt, mời các em tham khảo thêm các dạng bài tập Toán lớp 7 tại chuyên mục Giải Toán 7 Tập 2 CTST do GiaiToan biên soạn để ôn tập nhé.