Giaitoan.com Toán 9 Luyện tập Toán 9 Chuyên đề Toán 9 thi vào 10

Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF) Chuyên đề Toán 9 thi vào 10

Nội dung
  • 1 Đánh giá

Chứng minh tứ giác nội tiếp

Bài tập Toán 9: Tứ giác nội tiếp được GiaiToan biên soạn bao gồm đáp án chi tiết cho từng bài tập giúp các bạn học sinh ngoài bài tập trong sách giáo khoa (sgk) có thể luyện tập thêm các dạng bài tập cơ bản và nâng cao Toán hình lớp 9. Đây là tài liệu tham khảo hay dành cho quý thầy cô và các vị phụ huynh lên kế hoạch ôn tập học kì môn Toán 9 và ôn tập thi vào lớp 10. Mời các bạn học sinh và quý thầy cô cùng tham khảo tài liệu chi tiết!

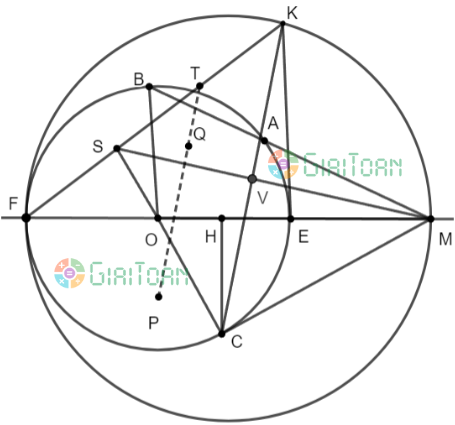
Bài tập: Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).

a) Chứng minh rằng MA . MB = ME . MF

b) Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.

c) Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.

d) Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng.

Lời giải chi tiết:

a) Vì ta có do hai tam giác đồng dạng MAE và MBF

Nên \frac{{MA}}{{ME}} = \frac{{MF}}{{MB}}\Rightarrow MA . MB = ME . MF

(Phương tích của M đối với đường tròn tâm O)

b) Áp dụng hệ thức lượng trong đường tròn, ta có MA . MB = MC2,

Mặt khác, tam giác vuông MCO có đường cao CH, ta có:

MH . MO = MC2 (hệ thức lượng trong tam giác vuông)

\Leftrightarrow MA . MB = MH . MO

nên tứ giác AHOB nội tiếp trong đường tròn.

c) Xét tứ giác MKSC nội tiếp trong đường tròn đường kính MS (có hai góc K và C vuông).

Vậy ta có : MK2 = ME . MF = MC2 nên MK = MC.

Do đó MF chính là đường trung trực của KC

Suy ra MS vuông góc với KC tại V.

d) Do hệ thức lượng trong đường tròn ta có MA . MB = MV . MS của đường tròn tâm Q.

Tương tự với đường tròn tâm P, ta cũng có MV . MS = ME . MF

Suy ra PQ vuông góc với MS và là đường trung trực của VS (đường nối hai tâm của hai đường tròn).

Do đó PQ cũng đi qua trung điểm của KS (do định lí trung bình của tam giác SKV).

Vậy 3 điểm T, Q, P thẳng hàng.

Tứ giác nội tiếp là gì?

- Tứ giác nội tiếp đường tròn là tứ giác có bôn đỉnh nằm trên một đường tròn. Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.

Cách chứng minh tứ giác nội tiếp

Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cách đều 1 điểm

Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800)

Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.

Tham khảo tài liệu chi tiết: Hướng dẫn phương pháp chứng minh tứ giác nội tiếp

---------------------------------------------

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 80
Tìm thêm: Chuyên đề Toán 9 Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần