Toán thực tế - Hình học không gian Chuyên đề Toán 9 thi vào 10

1 Đánh giá

Toán thực tế - Hình học không gian

Bài toán thực tế về hình học không gian là tài liệu do GiaiToan sưu tầm và biên soạn với lời giải chi tiết cho dạng bài liên quan đến hình học không gian và các công thức liên quan giúp các bạn học sinh nắm vững các kiến thức và áp dụng tính toán trong các bài tập. Mời các bạn học sinh cùng tham khảo bài viết.

A. Công thức tính diện tích, thể tích các hình không gian

1. Hình trụ

Nếu hình trụ có bán kính đáy R và chiều cao h thì:

+ Diện tích xung quanh: $S_{xq} = πRh$

+ Diện tích toàn phần: $S_{tp} = 2πRh + 2πR^{2}$

+ Thể tích: $V = πR^{2} h$

2. Hình cầu

Nếu hình cầu có bán kính R thì:

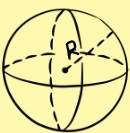
+ Diện tích mặt cầu: $S = 4πR^{2}$

+ Thể tích hình cầu: $V = \frac{4}{3}πR^{2}$

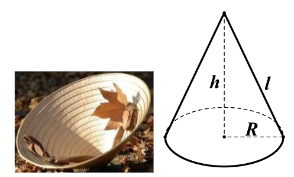
3. Hình nón

Nếu Hình nón có bán kính đáy R, chiều cao h và đường sinh l thì:

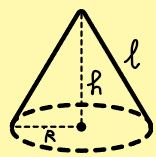
+ Diện tích xung quanh: $S_{xq} = 2πRl$

+ Diện tích toàn phần: $S_{tp} = πRl + πR^{2}$

+ Thể tích: $V= \frac{1}{3} πR^{2} h$

4. Hình nón cụt

Nếu Hình nón cụt bán kính đáy lớn R, bán kính đáy nhỏ r, chiều cao h và đường sinh l thì:

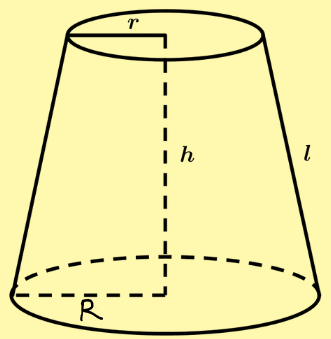
+ Diện tích xung quanh: $S_{xq} = π(R + r)l$

+ Diện tích toàn phần: $S_{tp} = π(R + r)l + πR^2 + πr^2$

+ Thể tích: $V= \frac{1}{3} πh (R^{2} + Rr + r^{2} )$

B. Bài tập ví dụ

Ví dụ 1: Một quả bóng bàn dạng một hình cầu có bán kính bằng 2 cm. Tính diện tích bề mặt của quả bóng bàn đó (lấy π ≈ 3,14).

Lời giải chi tiết:

Vì quả bóng bàn hình cầu có bán kính R = 2 cm nên diện tích bề mặt quả bóng là:

S_{bề mặt} = 4πR² = 4. 3,14 . 2² ≈ 50,24 (cm²)

Vậy diện tích bề mặt quả bóng bàn là 50,24 cm².

Ví dụ 2: Một bồn nước inox có dạng hình trụ với chiều cao 1,75 m và diện tích đáy là 0,32 m². Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn).

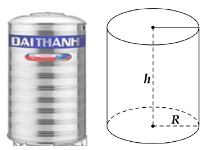
Lời giải chi tiết:

Bồn nước hình trụ có chiều cao h = 1,75 m và diện tích đáy S_đáy = 0,32 m² nên thể tích của bồn là:

V_bồn = S_đáy . h = 0,32 . 1,75 = 0,56 m³.

Vậy bồn đựng đầy nước thì được 0,56 m³ nước.

Ví dụ 3: Một chiếc nón có bán kính đáy bằng 15 cm và chiều cao bằng 20 cm. Hỏi chiếc nón múc đầy được bao nhiêu cm³ nước (lấy π = 3,14).

Lời giải chi tiết:

Chiếc nón có bán kính đáy R = 15 cm và chiều cao h = 20 cm nên thể tích của chiếc nón là:

$V_{nón}=\frac{1}{3}\pi R^2h=\frac{1}{3}.3,14.15^2.20=4710$ (cm³)

Vậy chiếc nón múc đầy được 4710 cm³ nước.

C. Bài tập tự luyện

Bài 1: Một quả bóng bằng da có đường kính 22 cm. Tính diện tích da cần dùng để làm quả bóng nếu không tính tỉ lệ hao hụt (lấy π = 3,14).

Xem lời giải chi tiết

Bài 2: Bác An có một đống cát hình nón cao 2 m, đường kính đáy 6 m; bác tính rằng để sửa xong ngôi nhà của mình cần 30 m³ cát. Hỏi bác An cần mua bổ sung bao nhiêu m³ cát nữa để đủ cát sửa nhà (lấy π = 3,14 và các kết quả làm tròn đến chữ số thập phân thứ hai).

Xem lời giải chi tiết

Bài 3: Một thùng nước hình trụ có chiều cao bằng đường kính đáy và bằng 1 m. Thùng nước này có thể đựng được 1 m³ nước không? Tại sao? (lấy π = 3,14).

Xem lời giải chi tiết

Bài 4: Người ta dự định làm dự định làm một chiếc bồn chứa dầu bằng sắt hình trụ có chiều cao 1,8 m, đường kính đáy 1,2 m. Hỏi chiếc bồn đó chứa đầy được bao nhiêu lít dầu, biết rằng 1 m³ = 1000 lít (Bỏ qua bề dày của bồn; lấy π = 3,14).

Xem lời giải chi tiết

Bài 5: Trái Đất, hành tinh chúng ta đang sống, dạng hình cầu có bán kính là 6370 km. Biết rằng 29% diện tích bề mặt Trái Đất không bị bao phủ bởi nước bao gồm núi, sa mạc, cao nguyên, đồng bằng và các địa hình khác. Tính diện tích bề mặt mặt Trái Đất bị bao phủ bởi nước (Lấy π = 3,14; kết quả làm tròn đến chữ số hàng đơn vị).

Xem lời giải chi tiết

Bài 6: Một hộp đựng chè hình trụ có đường kính đáy bằng 8 cm và chiều cao bằng 12 cm. Tính diện tích giấy carton để làm một hộp chè đó, biết tỉ lệ giấy carton hao hụt khi làm một hộp chè là 5% (lấy π = 3,14).

Xem lời giải chi tiết

Bài 7: Một cốc thủy tinh hình trụ đựng đầy nước có chiều cao bằng 10 cm và thể tích bằng 90π cm³. Người ta thả vào cốc một viên bi sắt hình cầu có bán kính bằng bán kính đáy cốc nước, viên bi sắt ngập toàn bộ trong nước. Tính lượng nước bị tràn ra khỏi cốc?

Xem lời giải chi tiết

Bài 8: Một chiếc xô có hình dạng là một hình nón cụt bán kính đáy lớn bằng 19 cm, bán kính đáy nhỏ bằng 13 cm, chiều cao là 25 cm. Hỏi chiếc xô đựng đầy được bao nhiêu cm³ nước (lấy π = 3,14).

Xem lời giải chi tiết

----------------------------------------

Chia sẻ bởi: