Giaitoan.com Toán 12

Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính Công thức Toán 12

Nội dung
  • 3 Đánh giá

Bài tập Toán 12: Tìm giá trị lớn nhất nhỏ nhất

Cách tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức về cách bấm máy tính tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số Toán THPT. Tài liệu bao gồm công thức, cách bấm máy tính, bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề Hàm số lớp 12. Chúc các bạn học tập hiệu quả!

A. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số

Phương pháp:

Bước 1: Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên miền [a; b] ta sử dụng máy tính Casio với lệnh MODE 7 (lập bảng giá trị).

Bước 2: Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất là min.

Chú ý:

+ Ta thiết lập miền giá trị của biến x Start a End B Step \frac{{b - a}}{{19}} (có thể làm tròn để Step đẹp).

+ Khi đề bài có các yếu tố lượng giác sinx, cosx, tanx, cotx, … ta chuyển máy tính về chế độ Radian.

B. Hướng dẫn tìm Min, Max bằng máy tính

Ví dụ 1: Hàm số y = |3cosx – 4sinx + 8| với x \in \left[ {0;2\pi } \right]. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Khi đó tổng M + m bằng bao nhiêu?

A. 8\sqrt 2

B. 7\sqrt 3

C. 8\sqrt 3

D. 16

Hướng dẫn giải

Cách 1: Bấm máy tính Casio

Bước 1: Để tính các bài toán liên quan đến lượng giác ta chuyển máy tính về chế độ Radian

SHIFT + MODE + 4

Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính

Bước 2: Sử dụng chức năng MODE 7 của máy tính Casio nhập hàm số ta được:

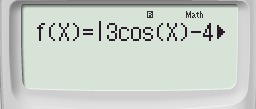
Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính

Bấm giá trị tuyệt đối bằng tổ hợp phím SHIFT + hyp

Bước 3: Thiết lập Start 0 End 2π Step \frac{{2\pi - 0}}{{19}} ta được bảng giá trị:

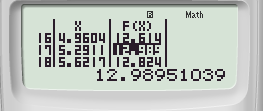
Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính

Quan sát bảng giá trị F(X) ta thấy giá trị lớn nhất F(X) có thể đạt được là f(5,2911) = 12,989 ≈ 13 = M

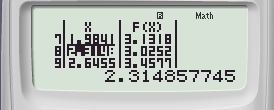
Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính

Giá trị nhỏ nhất F(X) có thể đạt được là f(2,3148) = 3,0252 ≈ 3 = m

Suy ra M + m = 16

Chọn đáp án D

Cách 2: Sử dụng bất đẳng thức

Áp dụng bất đẳng thức Bunhiacopski ta được:

Bất đẳng thức Bunhiacopxki

{\left( {ax + by} \right)^2} \leqslant \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right) . Dấu bằng xảy ra khi và chỉ khi \frac{a}{x} = \frac{b}{y}

{\left( {3\cos x - 4\sin x} \right)^2} \leqslant \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right) = 25

\Rightarrow \left| {3\cos x - 4\sin x} \right| \leqslant 5

\Rightarrow - 5 \leqslant 3\cos x - 4\sin x \leqslant 5

\Rightarrow 3 \leqslant 3\cos x - 4\sin x + 8 \leqslant 13

=> M = 13, m = 3

=> M + m = 16

Chọn đáp án D

Ví dụ 2: Cho các số x, y thỏa mãn điều kiện 0 ≤ y, {x^2} + x - y - 12 = 0. Tìm giá trị nhỏ nhất của biểu thức P = xy + x + 2y + 17

A. -12

B. -9

C. -15

D. -5

Hướng dẫn giải

Cách 1: Bấm máy tính Casio

Ta có: {x^2} + x - y - 12 = 0 \Rightarrow y = {x^2} + x - 12

Thay y vào P ta được biểu thức:

\begin{matrix} P = x\left( {{x^2} + x - 12} \right) + x + 2\left( {{x^2} + x - 12} \right) + 17 \hfill \\ P = \left( {x + 2} \right)\left( {{x^2} + x - 12} \right) + x + 17 \hfill \\ \end{matrix}

Bước 1: Để tìm Giá trị nhỏ nhất của P ta sử dụng chức năng lập bảng giá trị MODE 7, tuy nhiên bài toán khuyết thiếu miền giá trị của x. Để tìm được miền giá trị của x ta xét:

\begin{matrix} y \leqslant 0 \Rightarrow {x^2} + x - 12 \leqslant 0 \hfill \\ \Rightarrow - 4 \leqslant x \leqslant 3 \Rightarrow x \in \left[ { - 4;3} \right] \hfill \\ \end{matrix}

Bước 2: Sử dụng MODE 7 nhập hàm số ta được:

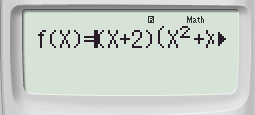
Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính

Bước 3: Thiết lập với Start -4 End 3 Start \frac{7}{{19}} ta được:

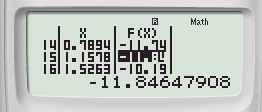
Cách tìm giá trị lớn nhất nhỏ nhất bằng máy tính

Giá trị nhỏ nhất F(X) có thể đạt được là f(1,1578) = -11,84 ≈ -12 = m

Chọn đáp án A

Cách 2: Làm bài tự luận

+ Dùng phương pháp dồn biến đưa biểu thức P chứa hai biến thành biểu thức P chứa 1 biến.

=> P = \left( {x + 2} \right)\left( {{x^2} + x - 12} \right) + x + 17 = {x^3} + 3{x^2} - 9x - 7

Đặt g\left( x \right) = {x^3} + 3{x^2} - 9x - 7

Tìm miền giá trị của biến ta có:

\begin{matrix} y \leqslant 0 \Rightarrow {x^2} + x - 12 \leqslant 0 \hfill \\ \Rightarrow - 4 \leqslant x \leqslant 3 \Rightarrow x \in \left[ { - 4;3} \right] \hfill \\ \end{matrix}

Khảo sát hàm số g(x) ta có:

g'\left( x \right) = 3{x^2} + 6x - 9 \Rightarrow g'\left( x \right) = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = 1} \\ {x = - 3} \end{array}} \right.

Ta có:

g\left( 1 \right) = - 12;g\left( { - 3} \right) = 20;g\left( { - 4} \right) = 13,g\left( 3 \right) = 20

Vậy giá trị nhỏ nhất của hàm số là -12 khi x = 1

Chọn đáp án A

C. Bài tập tự luyện tìm min, max của hàm số

Bài tập 1: Giá trị nhỏ nhất của hàm số y = \sqrt {1 + \sin x} + \sqrt {1 + \cos x} là:

A. \min y = 0

B. \min y = 1

C. \min y = \sqrt {4 - 2\sqrt 2 }

D. \min y \in \left\{ \emptyset \right\}

Bài tập 2: Cho hàm số y = 3sinx – 4sin3x. Giá trị lớn nhất của hàm số trên khoảng \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right) bằng:

A. 1

B. 7

C. -1

D. 3

Bài tập 3: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = (x2 – 3)ex trên đoạn [0; 2]. Giá trị của biểu thức P = {\left( {{m^2} - 4{M^2}} \right)^{2016}} là:

A. 0

B. {e^{2016}}

C. 1

D. {2^{2016}}

Bài tập 4: Tìm m để hàm số y = \frac{{mx - 4}}{{x + m}} đạt giá trị lớn nhất bằng 5 trên [-2; 6]

A. m = \frac{2}{6}

B. m = - \frac{4}{5}

C. m = \frac{3}{4}

D. m = \frac{6}{7}

----------------------------------------------------

Hi vọng Giá trị nhỏ nhất, giá trị lớn nhất của hàm số do GiaiToan giới thiệu là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Một số tài liệu liên quan:

Chia sẻ bởi: Kim Ngưu
Mời bạn đánh giá!
  • Lượt xem: 6.462
Tìm thêm: Toán 12 Chuyên đề Toán 12
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần