Giaitoan.com Toán 10 Toán 11 Toán 12

Sin3x = ? Công thức lượng giác

Nội dung
  • 12 Đánh giá

Công thức nhân ba sin 3x

Công thức lượng giác cơ bản đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức về dạng toán biến đổi công thức lượng giác 10, 11 và lớp 12. Tài liệu bao gồm công thức lượng giác, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề lượng giác. Chúc các bạn học tập hiệu quả!

Công thức nhân ba

A. Công thức sin 3x

Công thức:

sin 3x = 3sin x - 4sin3 x

Chứng minh

sin 3x = sin(2x + x)

= sin 2x.cos x + cos 2x.sin x

= 2sin x.cos x.cos x + (2cos2 x – 1).sin x

= 2sin x.cos2 x + 2cos2 x.sin x – sin x

= 4sin x.cos2 x – sin x

= 4sin x.(1 – sin2 x) – sin x

= 3sin x – 4sin3 x

=> Điều phải chứng minh.

B. Hàm số y = sin 3x

Tập xác định của hàm số y = sin 3x

Tập xác định D = \mathbb{R}

Tập giá trị của y = sin 3x

-1 ≤ sin 3x ≤ 1

=> Giá trị lớn nhất của y = sin 3x bằng 1

=> Giá trị nhỏ nhất của hàm số y = sin 3x bằng -1

Tính chẵn lẻ của hàm số y = sin 3x

Với x ∈ D => -x ∈ D ta có:

y = sin 3x

y(-x) = sin(- 3x) = - sin(3x)

=> y(x) = - y(- x)

=> Hàm số là hàm số lẻ

Vậy hàm số y = sin 3x là hàm số lẻ

Chu kì tuần hoàn của hàm số y = sin 3x

Hàm số y = sin 3x tuần hoàn với chu kì T = \frac{{2\pi }}{3}

Công thức mở rộng:

Hàm số y = sin(ax + b) tuần hoàn với chu kì T = \frac{{2\pi }}{{\left| a \right|}}

C. Đồ thị hàm số y = sin 3x

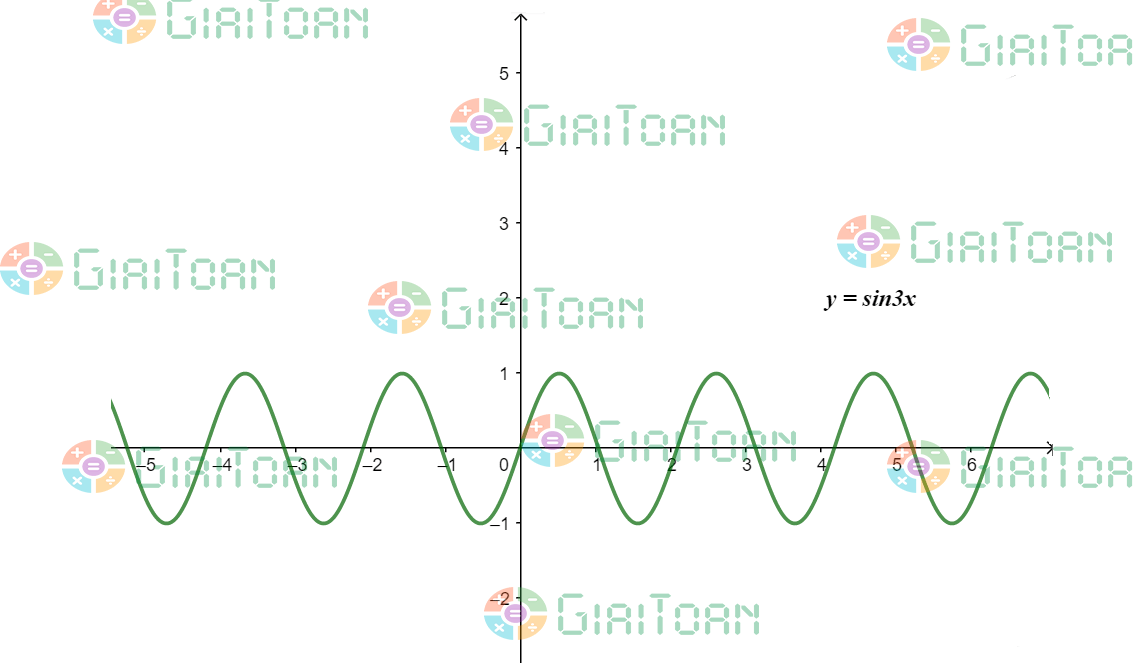
Sin3x

D. Đạo hàm sin 3x

y = sin 3x

=> y’ = (sin 3x)’

=> y’ = (3x)’ . [cos (3x)]

=> y’ = 3.cos (3x)

Vậy đạo hàm của y = sin 3x là y’ = 3cos (3x)

E. Nguyên hàm sin3x

\int {\sin 3xdx = \frac{1}{3}\int {\sin 3xd\left( {3x} \right) = - \frac{1}{3}\cos 3x + C} }

Vậy họ nguyên hàm của hàm số y = sin3x là \int {\sin 3xdx = - \frac{1}{3}\cos 3x + C}

f. Công thức lượng giác thường gặp

G. Phương trình lượng giác thường gặp

-------------------------------------------------

Hi vọng Chuyên đề công thức lượng giác là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Một số tài liệu liên quan:

Chia sẻ bởi: Bờm
Mời bạn đánh giá!
  • Lượt xem: 91.209
Tìm thêm: Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần