Giaitoan.com Toán 12

Cách tính nhanh đồng biến nghịch biến bằng máy tính Công thức Toán thi THPT Quốc Gia

Nội dung
  • 1 Đánh giá

Bài tập toán 12: Xét tính đơn điệu của hàm số

Tìm khoảng đồng biến, nghịch biến của hàm số bằng máy tính casio đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức về cách bấm máy tính tìm khoảng đồng biến, nghịch biến của hàm số Toán THPT. Tài liệu bao gồm công thức, cách bấm máy tính, bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề Hàm số lớp 12. Chúc các bạn học tập hiệu quả!

A. Hàm số đồng biến, Hàm số nghịch biến

Cho hàm số y = f(x) có đạo hàm trên khoảng P.

Nếu f’(x) ≥ 0 với moi x ∈ P và f’(x) = 0 tại hữu hạn điểm của P thì hàm số y = f(x) đồng biến hoặc nghịch biến trên P.

B. Cách bấm máy tính tìm khoảng đồng biến nghịch biến của hàm số

Cách 1: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính casio. Quan sát bằng kết quả nhận được, khoảng nào làm cho hàm số luôn tăng thì là khoảng đồng biến, khoảng nào làm cho hàm số luôn giảm là nghịch biến.

Cách 2: Tính đạo hàm, thiết lập phương trình đạo hàm, cô lập tham số m và đưa về dạng m ≥ f(x) hoặc m ≤ f(x). Tìm Min, Max của hàm số f(x) rồi kết luận.

Cách 3: Tính đạo hàm, thiết lập phương trình đạo hàm. Sử dụng tính năng giải bất phương trình INEQ của máy tính casio (đối với bất phương trình bậc hai, bậc ba).

C. Bài tập tìm khoảng đồng biến, nghịch biến của hàm số bằng máy tính

Ví dụ 1: Hàm số y = 2x4 + 1 đồng biến trên khoảng nào?

A. \left( { - \infty \frac{{ - 1}}{2}} \right)

B. \left( {0; + \infty } \right)

C. \left( { - \frac{1}{2}; + \infty } \right)

D. \left( { - \infty ;0} \right)

Hướng dẫn giải

Cách 1: Sử dụng MODE 7 lập bảng giá trị

Để kiểm tra đáp án A ta sử dụng chức năng lập bảng giá trị MODE 7 với thiết lập START -10 END -0,5 STEP 0,5 ta được

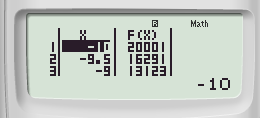
Cách tính nhanh đồng biến nghịch biến bằng máy tính

Quan sát bảng giá trị ta thấy x càng tăng thì f(x) càng giảm => Loại đáp án A.

Làm tương tự với các đáp án khác

Kiểm tra đáp án B với với thiết lập START 0 END 9 STEP 0,5 ta được

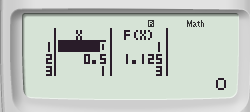
Cách tính nhanh đồng biến nghịch biến bằng máy tính

Quan sát bảng giá trị ta thấy x càng tăng thì f(x) cũng tăng => Đáp án B đúng.

Cách 2: Casio đạo hàm

Kiểm tra đáp án A khoảng \left( { - \infty \frac{{ - 1}}{2}} \right) ta tính đạo hàm của hàm số tại x = - \frac{1}{2} - 0,1

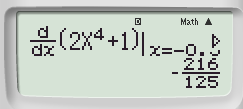
Bằng tổ hợp phím SHIFT Cách tính nhanh đồng biến nghịch biến bằng máy tính ta được

Cách tính nhanh đồng biến nghịch biến bằng máy tính

Đạo hàm ra âm (Hàm số nghịch biến) => Đáp án A sai.

Kiểm tra đáp án A khoảng \left( { - \infty ;0} \right) ta tính đạo hàm của hàm số tại x = 0 - 0,1

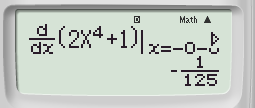
Bằng tổ hợp phím SHIFT Cách tính nhanh đồng biến nghịch biến bằng máy tính ta được

Cách tính nhanh đồng biến nghịch biến bằng máy tính

Đạo hàm ra âm (Hàm số nghịch biến) => Đáp án C, D sai

Chọn đáp án B

Kiểm tra lại đáp án B. Ta tính đạo hàm của hàm số tại x = 1 + 0,1

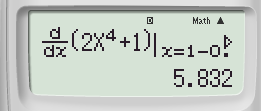
Bằng tổ hợp phím SHIFT Cách tính nhanh đồng biến nghịch biến bằng máy tính ta được

Cách tính nhanh đồng biến nghịch biến bằng máy tính

Vậy đáp án đúng là đáp án B.

Ví dụ 2: Hàm số y = {x^3} + 3{x^2} + mx + m đồng biến trên tập xác định khi giá trị của m là:

A. m ≤ 1

B. m ≥ 3

C. -1 ≤ m ≤ 3

D. m < 3

Hướng dẫn giải

Bước 1: Để giải các bài toán liên quan đến tham số m thì ta cần cô lập m.

Hàm số đồng biến khi và chỉ khi y’ ≥ 0 =>

Vậy để hàm số y đồng biến trên tập xác định thì hay m ≥ f(x) hay m ≥ f(max) với mọi giá trị x thuộc R.

Bước 2: Nhấn tổ hợp phím MODE 7 rồi nhập hàm số y ta được:

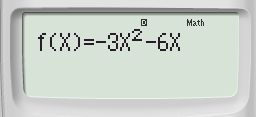
Cách tính nhanh đồng biến nghịch biến bằng máy tính

Bước 3: Thiết lập START -9 END 10 STEP 1:

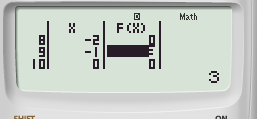
Cách tính nhanh đồng biến nghịch biến bằng máy tính

Quan sát bảng giá trị ta thấy

+ Giá trị lớn nhất có thể đạt được là f(-1) = 3

Vậy m ≥ 3

Chọn đáp án B

Ví dụ 3: Tìm tất cả các giá trị thực của m sao cho hàm số y = \frac{{\tan x - 2}}{{\tan x - m}} đồng biến trên khoảng \left( {0;\frac{\pi }{4}} \right)

A. \left[ {\begin{array}{*{20}{c}} {m \leqslant 0} \\ {1 \leqslant m < 2} \end{array}} \right.

B. m < 2

C. -1 ≤ m < 2

D. m ≥ 2

Hướng dẫn giải

Đưa máy tính về chế độ Radian bằng tổ hợp phím SHIFT MODE 4

Đơn giản bài toán bằng cách đặt tanx = t.

Chú ý khi đổi biến ta phải tìm miền giá trị của biến mới, ta sử dụng chức năng MODE 7 cho hàm y = tanx với thiết lập START 0 END π/4 STEP π/76 ta được

Ta thấy 0 ≤ tanx ≤ 1 => t ∈ (0; 1)

Bài toán trở thành bài toán tìm m để hàm số y = \frac{{\operatorname{t} - 2}}{{\operatorname{t} - m}} đồng biến trên khoảng (0; 1)

Tính đạo hàm của hàm số y' = \frac{{2 - m}}{{{{\left( {t - m} \right)}^2}}}

y' > 0 \Leftrightarrow \frac{{2 - m}}{{{{\left( {t - m} \right)}^2}}} > 0 \Leftrightarrow m < 2\left( * \right)

Kết hợp với điều kiện xác đinh t – m ≠ 0 => m ≠ t => m ∉ (0; 1) (**)

Từ (*) và (**) ta được \left[ {\begin{array}{*{20}{c}} {m \leqslant 0} \\ {1 \leqslant m < 2} \end{array}} \right. => Chọn đáp án A

----------------------------------------------------

Hi vọng Bấm máy tính tìm khoảng đồng biến, nghịch biến của hàm số do GiaiToan giới thiệu là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Chia sẻ bởi: Đội Trưởng Mỹ
Mời bạn đánh giá!
  • Lượt xem: 21.961
Tìm thêm: Toán 12 Chuyên đề Toán 12
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần