Lý thuyết Số thập phân Toán lớp 5
Toán lớp 5: Số thập phân
GiaiToan xin giới thiệu tới các em bài Lý thuyết Số thập phân. Bài học bao gồm lý thuyết bài tập kèm lời giải chi tiết, cùng với bài tập trắc nghiệm, tự luyện giúp các em rèn luyện kỹ năng giải Toán lớp 5. Mời các em tham khảo.
A. Lý thuyết về Số thập phân
1. Khái niệm số thập phân
Ta có: ![]() viết là 0,9 m, đọc là không phẩy chín mét.
viết là 0,9 m, đọc là không phẩy chín mét.
![]()
![]() viết là 1,14 m, đọc là một phẩy mười bốn mét.
viết là 1,14 m, đọc là một phẩy mười bốn mét.
Các số 0,9; 0,18 là các số thập phân.
2. Cấu tạo số thập phân
Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Ví dụ:
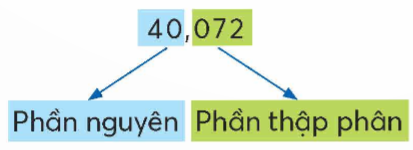
3. Hàng của số thập phân. Đọc, viết số thập phân
| Hàng trăm | Hàng chục | Hàng đơn vị | Hàng phần mười | Hàng phần trăm | Hàng phần nghìn | |
| 4 | 5 | 2 | , | 1 | 3 | 9 |
Số gồm 4 trăm, 5 chục, 2 đơn vị, 1 phần mười, 3 phần trăm, 9 phần nghìn.
Viết là: 452,139. Đọc là: Bốn trăm năm mươi hai phẩy một trăm ba mươi chín.
• Muốn đọc một số thập phân, ta đọc lần lượt từ hàng cao đến hàng thấp: trước hết đọc phần nguyên, đọc dấu “phẩy”, sau đó đọc phần thập phân.
• Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu “phẩy”, sau đó viết phần thập phân.
4. So sánh các số thập phân
a) Số thập phân bằng nhau
Nếu viết thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó.
Ví dụ: 1,23 = 1,230 = 1,23000
34 = 34,0 = 34,00 = 34,000
Lưu ý: Mỗi số tự nhiên a đều có thể viết thành số thập phân với phần thập phân là những chữ số 0.
Nếu một số thập phân có chữ số 0 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.
Ví dụ: 1,2300 = 1,230 = 1,23
34,000 = 34,00 = 34,0 = 34
b) So sánh hai số thập phân
• Nếu phần nguyên của hai số đó khác nhau thì số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
• Nếu phần nguyên của hai số đó bằng nhau thì so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn,...; đến một hàng nào đó, số thập phân có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
• Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Ví dụ:
218,1 > 215,99 (phần nguyên có 218 > 215).
85,135 < 85,2 (phần nguyên bằng nhau, hàng phần mười có 1 < 2).
156,47 > 156,426 (phần nguyên và hàng phần mười bằng nhau, hàng phần trăm có 4 > 2).
5. Làm tròn số thập phân
a) Làm tròn số thập phân đến số tự nhiên gần nhất.
Khi làm tròn số thập phân đến số tự nhiên gần nhất, ta so sánh chữ số ở hàng phần mười với 5. Nếu chữ số hàng phần mười bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.
Ví dụ:

b) Làm tròn số thập phân đến hàng phần mười, hàng phần trăm.
• Khi làm tròn số thập phân đến hàng phần mười, ta so sánh chữ số hàng phần trăm với 5. Nếu chữ số hàng phần trăm bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.
• Khi làm tròn số thập phân đến hàng phần trăm, ta so sánh chữ số hàng phần nghìn với 5. Nếu chữ số hàng phần nghìn bé hơn 5 thì làm tròn xuống, còn lại thì làm tròn lên.
Ví dụ:

B. Bài tập trắc nghiệm
C. Bài tập tự luyện
----------------------------------------
---> Tham khảo thêm:
Lý thuyết Viết số đo đại lượng dưới dạng số thập phân
Lý thuyết Phép cộng số thập phân
Lý thuyết Phép trừ số thập phân
Lý thuyết phép nhân số thập phân




























