Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật Toán lớp 5 trang 109

GiaiToan xin giới thiệu tới các em bài Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật. Nội dung bài bao gồm các dạng bài toán hình học và các dạng bài tập tự luyện kèm theo đáp án, giúp các em rèn luyện kỹ năng giải Toán 5, ôn tập chương 3 Toán 5. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

1. Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật Toán 5

a) Định nghĩa

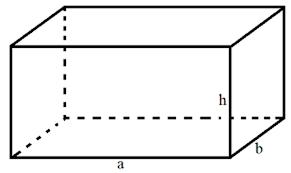
- Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.

- Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.

b) Quy tắc: Giả sử hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là h.

- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).

S_xq = (a + b) x 2 x h

- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

S_tp = S_xq + S_day x 2 = (a + b) x 2 x h + 2 x a x b

Lưu ý:

- Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với 2.

- Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.

Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.

Phương pháp:

- Ba kích thước của hình hộp chữ nhật có cùng đơn vị đo nên để tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao.

- Tính diện tích một đáy ta lấy chiều dài nhân với chiều rộng.

- Tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

Giải:

Chu vi đáy của hình hộp chữ nhật là:

(8 + 6) x 2 = 28 (cm)

Diện tích xung quanh của hình hộp chữ nhật đó là:

28 x 4 = 112 (cm²)

Diện tích một đáy là:

8 x6 = 48 (cm²)

Diện tích toàn phần của hình hộp chữ nhật đó là:

112 + 48 x 2 = 208 (cm²)

Đáp số: Diện tích xung quanh: 112cm²;

Diện tích toàn phần: 208cm².

Chú ý: Khi tìm diện tích xung quanh ta có thể làm gộp thành:(8 + 6) x 2 x 4 = 112 cm²

2. Một số dạng bài tập

Dạng 1: Tính diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật

Phương pháp: Áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.

Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật.

Phương pháp:

*) Từ công thức S_xq = (a + b) x 2 x h:

- Tìm chiều cao htheo công thức: h = S_xq : [(a + b) x 2] = S_xq : (a + b) : 2;

- Tìm tổng chu vi đáy theo công thức: (a + b) x 2 = S_xq : h.

*) Nếu biết diện tích toàn phần ta cũng thay vào công thức để tìm các đại lượng chưa biết.

Dạng 3: Toán có lời văn (thường là tìm diện tích hộp, căn phòng, sơn tường …)

Phương pháp: Cần xác định xem diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần rồi áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.

3. Giải bài tập Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

• Giải Toán lớp 5 trang 110
• Giải Toán lớp 5 trang 110 Luyện tập

>> Bài tiếp theo: Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình lập phương

Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật được GiaiToan chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, củng cố kiến thức cũng như chuẩn bị tốt cho bài kiểm tra Toán lớp 5 sắp tới. Chúc các em học tốt, ngoài việc tham khảo tài liệu trên các em cũng có thể tham khảo thêm Lý thuyết Toán lớp 5, Giải Toán Lớp 5, Luyện Tập Toán Lớp 5, Vở Bài Tập Toán Lớp 5 được GiaiToan biên soạn nhé

• Lý thuyết Hình hộp chữ nhật. Hình lập phương
• Lý thuyết Luyện tập về diện tích các hình lớp 5
• Lý thuyết Diện tích hình tròn
• Lý thuyết Hình tròn. Đường tròn. Chu vi hình tròn