Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 9 Đề thi cuối kì 1 lớp 8
Đề thi học kì 1 Toán 8 - Đề số 9
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 9 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 8 giúp học sinh ôn tập, củng cố kiến thức, để hoàn thành tốt bài thi cuối học kỳ 1. Mời các bạn cùng tham khảo chi tiết.
A. Đề thi Toán kì 1 lớp 8
Câu 1: Phân tích đa thức thành nhân tử
| a) | b) | c) |
Câu 2: Tìm x biết
| a) | b) | d) |
Câu 3: Cho biểu thức 
a) Tìm điều kiện xác định và rút gọn biểu thức P
b) Tìm các giá trị nguyên của x để P có giá trị nguyên dương
Câu 4: Cho tam giác ABC có 3 góc nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. K là điểm đối xứng với H qua M
a) Chứng minh BHCK là hình bình hành
b) Chứng minh ![]() và
và ![]()
c) Gọi I là điểm đối xứng với H qua BC. Chứng minh tứ giác BIKC là hình thang cân
d) BK cắt HI tại G. Tam giác ABC phải có điều kiện gì để tứ giác GHCK là hình thang cân
Câu 5: Tính giá trị của biểu thức

B. Đáp án Đề thi Toán kì 1 lớp 8
Câu 1
a)

b)

c)

Câu 2
a)

Vậy x = 0 hoặc x = 4
b)

Vậy x = 2 hoặc x = - 3
c)
![\begin{array}{l}
{x^3} + 27 + \left( {x + 3} \right)\left( {x - 9} \right) = 0\\
\Leftrightarrow {x^3} + 27 + {x^2} - 6x - 27 = 0\\
\Leftrightarrow {x^3} + {x^2} - 6x = 0\\
\Leftrightarrow x\left( {{x^2} + x - 6} \right) = 0\\
\Leftrightarrow x\left( {{x^2} + 3x - 2x - 6} \right) = 0\\
\Leftrightarrow x\left[ {x\left( {x + 3} \right) - 2\left( {x + 3} \right)} \right] = 0\\
\Leftrightarrow x\left( {x - 2} \right)\left( {x + 3} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x - 2 = 0\\
x + 3 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 2\\
x = - 3
\end{array} \right.
\end{array}](https://t.vdoc.vn/data/image/holder.png)
Vậy x = 0, x = 2 hoặc x = -3
Câu 3
a)
ĐKXĐ của P : 


b)
![]()
Để P nguyên thì ![]()
Ta có bảng sau:
| x + 3 | 1 | -1 | 3 | -3 | 9 | -9 |
| x | -2 | -4 | 0 | -6 | 6 | -12 |
| TM | Loại | TM | Loại | TM | Loại |
Vậy để P nhận giá trị nguyên dương thì ![]()
Câu 4
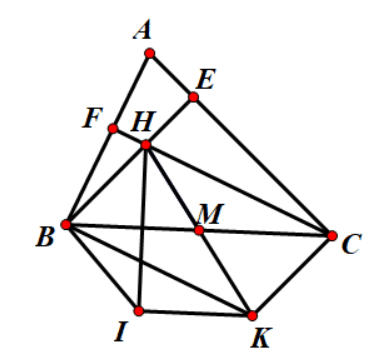
a)
Ta có
HM = MK ( H và K đối xứng với nhau qua M)
MB = MC ( M là trung điểm của BC )
![]() BHKC là hình bình hành ( hai đường chéo cắt nhau tại trung điểm mỗi đường)
BHKC là hình bình hành ( hai đường chéo cắt nhau tại trung điểm mỗi đường)
b)
Ta có
BK // HC ( tính chất hình bình hành)
Mà
![]() ( H là trực tâm tam giác ABC )
( H là trực tâm tam giác ABC )
![]()
Lại có
HB // CK ( BHKC là hình bình hành)
Mà
![]()
![]()
c)
Gọi D là giao điểm của BC và HI
![]() D là trung điểm của HI
D là trung điểm của HI
Mà
M là trung điểm của HK
![]() DM là đường trung bình của tam giác HIK
DM là đường trung bình của tam giác HIK
![]() hay
hay ![]() (1)
(1)
Lại có
BK = IC ( = HC) (2)
Từ (1) và (2) ta được BIKC là hình thang cân
d)
Ta có:
GK // HC
![]() GHCK là hình thang
GHCK là hình thang
Để GHCK là hình thang cân thì cần thêm điều kiện là 2 góc kề 1 đáy bằng nhau
Giả sử ![]()
Mà
![]() ( hai góc so le trong, CK // HE)
( hai góc so le trong, CK // HE)
![]()

![]() CH là phân giác của
CH là phân giác của
Mặt khác CH là đường cao
![]() ABC cân tại C
ABC cân tại C
Câu 5

Tài liệu liên quan
- Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 5
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 7
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 3
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 4
-------------------------------------------------------------------
Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 9. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Lý thuyết Toán 8, Giải Toán 8, Đề thi học kì 1 Toán 8, ....




























