Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 4 Đề thi cuối kì 1 lớp 8
Đề thi học kì 1 Toán 8 - Đề số 4
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 4 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 8 giúp học sinh ôn tập, củng cố kiến thức, để hoàn thành tốt bài thi cuối học kỳ 1. Mời các bạn cùng tham khảo chi tiết.
A. Đề thi Toán kì 1 lớp 8
Câu 1
1. Thực hiện phép tính
| a) | b) |
2. Tìm x biết
| a) | b) |
Câu 2: Phân tích đa thức thành nhân tử
| a) | b) |
Câu 3: Chứng tỏ rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến

( với ![]() )
)
Câu 4: Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP
a) Chứng minh tứ giác MDHE là hình chữ nhật
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông
c) Tam giác MNP cần thêm điều kiện gì để DE = 2 EA
B. Đáp án Đề thi Toán kì 1 lớp 8
Câu 1
1.
a)
![]()
b)
![]()
2.
a)

Vậy 
b)

Vậy x = 1 hoặc x = 2
Câu 2
a)
![]()
b)

Câu 3
Ta có


Vậy giá trị của biểu thức A không phụ thuộc vào biến x
Câu 4
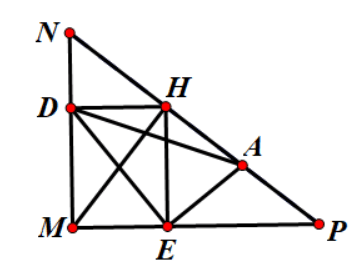
a)
Ta có:
![]() ( tam giac NMP vuông tại M)
( tam giac NMP vuông tại M)
![]()
![]()
![]()
Nên DHME là hình chữ nhật ( tứ giác có 3 góc vuông )
b) Gọi O là giao điểm của DE và MH
![]()
Xét tam giác EHP vuông tại E có:
![]() ( tính chất đường trung tuyến của tam giác vuông)
( tính chất đường trung tuyến của tam giác vuông)
![]()
![]()
Mà: ![]()
Nên ![]() hay tam giác DAE vuông tại E
hay tam giác DAE vuông tại E
c)
Để DE = 2EA thì ![]() tam giác OEA vuông cân
tam giác OEA vuông cân
![]()
![]() MDHE là hình vuông
MDHE là hình vuông
![]() MH là phân giác của góc M
MH là phân giác của góc M
Mà MH là đường cao
![]() Tam giác MNP vuông cân tại M
Tam giác MNP vuông cân tại M
-----------------------------------------------------------------------
Tài liệu liên quan
- Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 2
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 1
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 3
Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 5
Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 4. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Lý thuyết Toán 8, Giải Toán 8, Đề thi học kì 1 Toán 8, ....




























