Giaitoan.com Toán 8 Đề thi học kì 1 lớp 8

Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 6 Đề thi cuối kì 1 lớp 8

Nội dung
  • 1 Đánh giá

Đề thi học kì 1 Toán 8 - Đề số 6

Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 6 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 8 giúp học sinh ôn tập, củng cố kiến thức, để hoàn thành tốt bài thi cuối học kỳ 1. Mời các bạn cùng tham khảo chi tiết.

A. Đề thi Toán kì 1 lớp 8

I. Phần trắc nghiệm

Câu 1: Kết quả của phép nhân 2x\left( {x - 5} \right)  là

A. 2{x^2} - 5B. 2{x^2} - 10xC. 10x - 2{x^2}D. 2{x^2} - 10


Câu 2: Kết quả của phép khai triển {\left( {x - 2} \right)^2} là

A. {x^2} + 2x + 4B. {x^2} - 2x - 4C. {x^2} - 4x - 4D. {x^2} - 4x + 4

Câu 3: Rút gọn phép tính \dfrac{{{x^2} - 8x + 7}}{{\left( {7 - x} \right)\left( {x + 2} \right)}} là

A. \dfrac{{x - 1}}{{x + 2}}B. \dfrac{{x + 1}}{{x + 2}}C. \dfrac{{x - 1}}{{2 - x}}D. \dfrac{{1 - x}}{{x + 2}}


Câu 4: Tứ giác nào sau đây có hai đường chéo bằng nhau

A. Hình bình hànhB. Hình chữ nhật
C. Hình thangD. Hình thoi


Câu 5: Cho hình ABCD. Khi đó:

A. AB \bot CDB. AB \bot BD
C. AC là phân giác của góc AD. AC = BD


Câu 6: Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10 cm, thì diện tích tam giác ABC là:

A. 60\left( {c{m^2}} \right)B. 30\left( {c{m^2}} \right)C. 48\left( {c{m^2}} \right)D. 24\left( {c{m^2}} \right)


Câu 7: Cho hình bình hành ABCD có  \widehat A = {80^ \circ }. Tính số đo góc C

A. \widehat C = {80^ \circ }B. \widehat C = {100^ \circ }C. \widehat C = {40^ \circ }D. \widehat C = {160^ \circ }


II. Phần tự luận

Câu 1

a) 2x{y^2} - 4yb) {x^2}y - 6xy + 9y
c) {x^2} + x - {y^2} - yd) {x^2} + 4x + 3

Câu 2: Cho biểu thức P = \dfrac{{2{x^2} - 1}}{{{x^2} + x}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}}

a) Tìm điều kiện xác định của P

b) Rút gọn biểu thức P

c) Tính giá trị của biểu thức P khi x thỏa mãn  {x^2} - x = 0

Câu 3: Cho hình chữ nhật ABCD. Gọi E, F là trung điểm của AB và CD

a) Tứ giác AEFC là hình gì

b) Chứng minh AEFD là hình chữ nhật

c) Vẽ M là điểm đối xứng với F qua D, N là điểm đối xứng với A qua D. Chứng minh tứ giác ANMF là hình thoi

d) Gọi I,K là giao điểm của BD với AF, EF. Chứng minh

Câu 4: Cho \dfrac{{{x^2}}}{{x + y}} + \dfrac{{{y^2}}}{{y + z}} + \dfrac{{{z^2}}}{{z + x}} = 2017 . Tính giá trị của biểu thức

P = \dfrac{{{y^2}}}{{x + y}} + \dfrac{{{z^2}}}{{y + z}} + \dfrac{{{x^2}}}{{z + x}} - 3

B. Đáp án Đề thi Toán kì 1 lớp 8

I. Phần trắc nghiệm

1. B2. D3. D4. B5. B6.D7. B

II. Phần tự luận

Câu 1

a)

2x{y^2} - 4y = 2y\left( {xy - 2} \right)

b)

{x^2}y - 6xy + 9y = y\left( {{x^2} - 6x + 9} \right) = y{\left( {x - 3} \right)^2}

c)

\begin{array}{l} {x^2} + x - {y^2} - y\\ = \left( {{x^2} - {y^2}} \right) + \left( {x - y} \right)\\ = \left( {x - y} \right)\left( {x + y} \right) + \left( {x - y} \right)\\ = \left( {x - y} \right)\left( {x + y + 1} \right) \end{array}

d)

\begin{array}{l} {x^2} + 4x + 3\\ = {x^2} + 3x + x + 3\\ = x\left( {x + 3} \right) + \left( {x + 3} \right)\\ = \left( {x + 1} \right)\left( {x + 3} \right) \end{array}

Câu 2

a)

Điều kiện xác định của P:  \left\{ \begin{array}{l} {x^2} + x \ne 0\\ x \ne 0\\ x + 1 \ne 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x\left( {x + 1} \right) \ne 0\\ x \ne 0\\ x + 1 \ne 0 \end{array} \right. \Leftrightarrow \Leftrightarrow \left\{ \begin{array}{l} x \ne 0\\ x \ne - 1 \end{array} \right.

b)

\begin{array}{l} P = \dfrac{{2{x^2} - 1}}{{{x^2} + x}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}}\\ P = \dfrac{{2{x^2} - 1}}{{x\left( {x + 1} \right)}} - \dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} + \dfrac{{3x}}{{x\left( {x + 1} \right)}}\\ P = \dfrac{{2{x^2} - 1 - \left( {x - 1} \right)\left( {x + 1} \right) + 3x}}{{x\left( {x + 1} \right)}}\\ P = \dfrac{{2{x^2} - 1 - {x^2} + 1 + 3x}}{{x\left( {x + 1} \right)}}\\ P = \dfrac{{{x^2} + 3x}}{{x\left( {x + 1} \right)}}\\ P = \dfrac{{x\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}}\\ P = \dfrac{{x + 3}}{{x + 1}} \end{array}

c) 

\begin{array}{l} {x^2} - x = 0 \Leftrightarrow x\left( {x - 1} \right) = 0\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x - 1 = 0 \end{array} \right.\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l} x = 0\,\,\,\,\left( l \right)\\ x = 1 \end{array} \right. \end{array}

Với x = 1 thay vào P ta được

P = \dfrac{{x + 3}}{{x + 1}} \Rightarrow P = \dfrac{{1 + 3}}{{1 + 1}} = 2

Câu 3


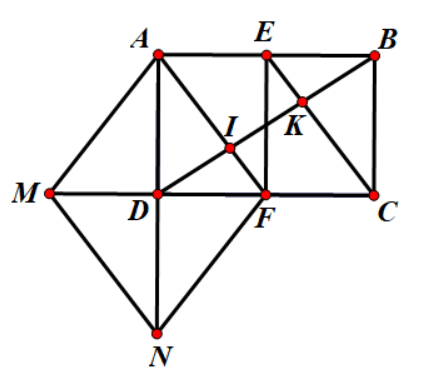
a)

Ta có: AB = CD ( do ABCD là hình chữ nhật)

Mà

\left\{ \begin{array}{l} AE = BE = \dfrac{1}{2}AB\\ CF = DF = \dfrac{1}{2}DC \end{array} \right. \Rightarrow AE = AF

( E, F lần lượt là trung điểm của AB và DC)

Lại có:

AE // AF

AECF là hình bình hành

b)

Ta có AB = CD ( do ABCD là hình chữ nhật)

Mà

\left\{ \begin{array}{l} AE = BE = \dfrac{1}{2}AB\\ CF = DF = \dfrac{1}{2}DC \end{array} \right. \Rightarrow AE = DF

Lại có AE // DF

\RightarrowAEFD là hình bình hành

Mà \widehat {BAC} = {90^ \circ }

Nên AEFD là hình chữ nhật

c)

DM = DF ( M là điểm đối xứng với F qua D )

DN = DA ( N là điểm đối xứng với A qua D)

Mà AN \bot MF

Vậy AMNF là hình thoi

d)

Xét tam giác DCK có:

E là trung điểm của AB

FI // CK

\Rightarrow I là trung điểm của DK hay IK = ID (1)

Xét tam giác BAI có:

F là trung điểm của DC

EK // AI

Do đó K là trung điểm của BI hay IK = BK (2)

Từ (1) và (2) \Rightarrow ID = IK = BK = \dfrac{1}{3}DK

Vậy IK = \dfrac{1}{3}DK

Câu 4

\begin{array}{l} \dfrac{{{x^2}}}{{x + y}} + \dfrac{{{y^2}}}{{y + z}} + \dfrac{{{z^2}}}{{z + x}} = 2017\\ \Leftrightarrow \left( {\dfrac{{{x^2}}}{{x + y}} - x} \right) + \left( {\dfrac{{{y^2}}}{{y + z}} - y} \right) + \left( {\dfrac{{{z^2}}}{{z + x}} - z} \right) + \left( {x + y + z} \right) = 2017\\ \Leftrightarrow \dfrac{{ - xy}}{{x + y}} + \dfrac{{ - yz}}{{y + z}} + \dfrac{{ - xz}}{{z + x}} + \left( {x + y + z} \right) = 2017\\ P = \dfrac{{{y^2}}}{{x + y}} + \dfrac{{{z^2}}}{{y + z}} + \dfrac{{{x^2}}}{{z + x}} - 3\\ = \left( {\dfrac{{{y^2}}}{{x + y}} - y} \right) + \left( {\dfrac{{{z^2}}}{{y + z}} - z} \right) + \left( {\dfrac{{{x^2}}}{{z + x}} - x} \right) + \left( {x + y + x} \right) + 3\\ = 2017 + 3 = 2020 \end{array}

Tài liệu liên quan

-------------------------------------------------------------------


Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 6. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Lý thuyết Toán 8, Giải Toán 8, Đề thi học kì 1 Toán 8, ....

  • 140 lượt xem
Chia sẻ bởi: Lê Thị Thùy
Tìm thêm: Toán 8 Đề thi học kì 1 Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Đề thi học kì 1 lớp 8