Giaitoan.com Toán 8 Đề thi học kì 1 lớp 8

Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 1 Đề thi cuối kì 1 lớp 8

Nội dung
  • 1 Đánh giá

Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 1

Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 1 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 8 giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết để hoàn thành tốt bài thi cuối học kỳ 1 . Mời các bạn cùng tham khảo chi tiết.

A. Đề thi Toán kì 1 lớp 8

Câu 1

1. Thực hiện phép tính

a. 2xy.3{x^2}{y^3}b. x\left( {{x^2} - 2x + 5} \right)
c. \left( {3{x^2} - 6x} \right):3xd. \left( {{x^2} - 2x + 1} \right):\left( {x - 1} \right)

2. Phân tích đa thức sau thành nhân tử

a. 5{x^3} - 5xb. {x^2} - 2xy + {y^2} - 4

Câu 2

Cho P = \left( {\dfrac{{x + 2}}{{2x - 4}} + \dfrac{{x - 2}}{{2x + 4}} - \dfrac{8}{{{x^2} - 4}}} \right):\dfrac{4}{{x - 2}}

a) Tìm ĐKXĐ của P

b) Rút gọn P

c) Tìm x để P = 2

Câu 3: Cho hai đa thức A = 2{x^3} + 5{x^2} - 2x + a và B = 2{x^2} - x + 1

a) Tính giá trị của biểu thức B khi x = -1

b) Tìm a để A chia hết cho B

Câu 4: Cho tam giác ABC vuông tại A và đường cao AH. Gọi D là điểm đối xứng với H qua AC. Gọi I là giao điểm của AB và DH, K là giao điểm của AC và HE

a) Tứ giác AIHK là hình gì?

b) Chứng minh rằng 3 điểm D, A, E thẳng hàng

c) Chứng minh BC = BD + CE

Câu 5: Cho các số x, y thỏa mãn đẳng thức:5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0

Tính giá trị của biểu thức

 M = {\left( {x + y} \right)^{2017}} + {\left( {x - 2} \right)^{2018}} + {\left( {y + 1} \right)^{2019}}

B. Đáp án Đề thi Toán kì 1 lớp 8

Câu 1

1.

a)

  2xy.3{x^2}{y^3} = 6{x^3}{y^4}

b)

x\left( {{x^2} - 2x + 5} \right) = {x^3} - 2{x^2} + 5x

c)

\left( {3{x^2} - 6x} \right):3x = x - 2

d)

\left( {{x^2} - 2x + 1} \right):\left( {x - 1} \right) = {\left( {x - 1} \right)^2}:\left( {x - 1} \right) = x - 1

2.

a)

5{x^3} - 5x = 5x\left( {{x^2} - 1} \right) = 5x\left( {x - 1} \right)\left( {x + 1} \right)

b)

\begin{array}{l} {x^2} - 2xy + {y^2} - 4 = \left( {{x^2} - 2xy + {y^2}} \right) - {2^2}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {x - y} \right)^2} - {2^2}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {x - y - 2} \right)\left( {x - y + 2} \right) \end{array}

Câu 2 

a)

ĐKXĐ của P: \left\{ \begin{array}{l} 2x - 4 \ne 0\\ 2x + 4 \ne 0\\ {x^2} - 4 \ne 0\\ x - 2 \ne 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ne - 2\\ x \ne 2 \end{array} \right.

b)

\begin{array}{l} P = \left( {\dfrac{{x + 2}}{{2x - 4}} + \dfrac{{x - 2}}{{2x + 4}} - \dfrac{8}{{{x^2} - 4}}} \right):\dfrac{4}{{x - 2}}\\ P = \left( {\dfrac{{x + 2}}{{2\left( {x - 2} \right)}} + \dfrac{{x - 2}}{{2\left( {x + 2} \right)}} - \dfrac{8}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right):\dfrac{4}{{x - 2}}\\ P = \left( {\dfrac{{\left( {x + 2} \right)\left( {x + 2} \right)}}{{2\left( {x - 2} \right)\left( {x + 2} \right)}} + \dfrac{{\left( {x - 2} \right)\left( {x - 2} \right)}}{{2\left( {x + 2} \right)\left( {x - 2} \right)}} - \dfrac{{8.2}}{{2.\left( {x - 2} \right)\left( {x + 2} \right)}}} \right):\dfrac{4}{{x - 2}}\\ P = \dfrac{{{x^2} + 4x + 4 + {x^2} - 4x + 4 - 16}}{{2\left( {x - 2} \right)\left( {x + 2} \right)}}.\frac{{x - 2}}{4}\\ P = \dfrac{{2{x^2} - 8}}{{2\left( {x - 2} \right)\left( {x + 2} \right)}}.\dfrac{{x - 2}}{4}\\ P = \dfrac{{2\left( {{x^2} - 4} \right)}}{{2\left( {x - 2} \right)\left( {x + 2} \right)}}.\dfrac{{x - 2}}{4}\\ P = \dfrac{{x - 2}}{4} \end{array}

c) Để P = 2 thì

\dfrac{{x - 2}}{4} = 2 \Leftrightarrow x - 2 = 8 \Leftrightarrow x = 10\,\,\left( {t/m} \right)

Vậy x = 10 thì P = 2

Câu 3

a)

Khi x = -1 thay vào B ta được: B = 2{\left( { - 1} \right)^2} - \left( { - 1} \right) + 1 = 4

b)

Ta có

2{x^3} + 5{x^2} - 2x + a = \left( {2{x^2} - x + 1} \right).\left( {x + 3} \right) + a - 3

Để A chia hết cho B thì a - 3 = 0 \Leftrightarrow a = 3

Câu 4

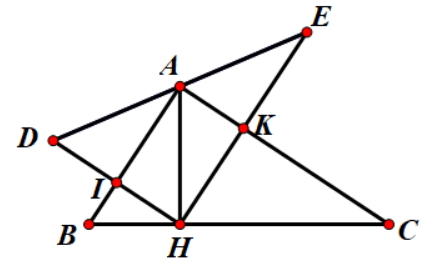
a)

Xét tứ giác AIHK có:

\widehat {IAK} = {90^ \circ }\left( {AB \bot AC} \right)

\widehat {AKH} = {90^ \circ }( E là điểm đối xứng với H qua AC)

\widehat {AIH} = {90^ \circ } (D là điểm đối xứng với H qua AB)

\Rightarrow \widehat {IAK} = \widehat {AKH} = \widehat {AIH} = {90^ \circ }

Nên AIHK là hình chữ nhật ( tứ giác có 3 góc vuông)

b)

Xét tam giác ADH có:

AB là đường cao đồng thời là đường trung tuyến

\Rightarrow \Delta ADH cân

\Rightarrow AB là đường phân giác của \widehat {DAH} \Rightarrow \widehat {DAB} = \widehat {BAH}

Xét tam giác AHE có:

 AC là đường cao đồng thời là đường trung tuyến

\Rightarrow \Delta AHE  cân

\Rightarrow AC là đường phân giác của \widehat {EAH} \Rightarrow \widehat {HAC} = \widehat {CAE}

Mà

\widehat {BAH} + \widehat {HAC} = {90^ \circ } \Rightarrow \widehat {BAD} + \widehat {EAC} = {90^ \circ } \Rightarrow DAE = {180^ \circ }

\Rightarrow 3 điểm D, A, E thẳng hàng

c)

Ta có

BC = BH + HC

Mà

\Delta BDH  cân tại B \Rightarrow BD = BH

Mà

\Delta ECH cân tại C \Rightarrow CE = CH

Nên

BC = BH + HC = BD + CE

Câu 5

Ta có

\begin{array}{l} 5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0\\ \Leftrightarrow \left( {4{x^2} + 4{y^2} + 8xy} \right) + {x^2} - 2x + 1 + {y^2} + 2y + 1 = 0\\ \Leftrightarrow 4\left( {{x^2} + {y^2} + 2xy} \right) + \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} + 2y + 1} \right) = 0\\ \Leftrightarrow 4{\left( {x + y} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 0 \end{array}

Vì

\begin{array}{l} \left\{ \begin{array}{l} 4{\left( {x + y} \right)^2} \ge 0\\ {\left( {x - 1} \right)^2} \ge 0\\ {\left( {y + 1} \right)^2} \ge 0 \end{array} \right.\forall x\\ \Rightarrow 4{\left( {x + y} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} \ge 0 \end{array}

Dấu “ =” xảy ra khi \left\{ \begin{array}{l} x = y\\ x = 1\\ y = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = - 1 \end{array} \right.

Thay vào M ta được:

M = {\left( {1 - 1} \right)^{2017}} + {\left( {1 - 2} \right)^{2018}} + {\left( { - 1 + 1} \right)^{2019}} = 1

 -----------------------------------------------------------------------

Tài liệu liên quan

  • Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 2
    Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 1
    Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 3
    Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 5


Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi học kì 1 Toán 8 năm học 2022 – 2023 - Đề số 1. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Lý thuyết Toán 8, Giải Toán 8, Đề thi học kì 1 Toán 8, ....

  • 587 lượt xem
Chia sẻ bởi: Lê Thị Thùy
Tìm thêm: Toán 8 Đề thi học kì 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan