Giaitoan.com Toán 11

Sinx = cosx Giải phương trình lượng giác

Nội dung
  • 7 Đánh giá

Giải phương trình lượng giác

Giải phương trình lượng giác sin x = cos x đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức về dạng toán giải phương trình Toán 11. Tài liệu bao gồm công thức lượng giác, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề phương trình lượng giác lớp 11. Chúc các bạn học tập hiệu quả!

A. Sin x – Cos x = ?

Công thức: \left\{ {\begin{array}{*{20}{c}} {\sin x - \cos x = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)} \\ {\sin x - \cos x = - \sqrt 2 \cos \left( {x + \dfrac{\pi }{4}} \right)} \end{array}} \right.

B. Giải phương trình sin x = cos x

Cách 1: Biến đổi về phương trình lượng giác cơ bản

sin x = cos x

\begin{matrix} \Leftrightarrow \sin x = \sin \left( {\dfrac{\pi }{2} - x} \right) \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \dfrac{\pi }{2} - x + k2\pi } \\ {x = \pi - \left( {\dfrac{\pi }{2} - x} \right) + k2\pi } \end{array}} \right. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {2x = \dfrac{\pi }{2} + k2\pi } \\ {x = \pi - \dfrac{\pi }{2} + x + k2\pi \left( L \right)} \end{array}} \right. \hfill \\ \Leftrightarrow x = \dfrac{\pi }{4} + k\pi ,\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}

Vậy phương trình lượng giác có nghiệm là x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)

Cách 2: Giải phương trình theo sin x

sin x = cos x

\begin{matrix} \Rightarrow \sin x - \cos x = 0 \hfill \\ \Rightarrow \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right) = 0 \hfill \\ \Rightarrow \sin \left( {x - \dfrac{\pi }{4}} \right) = 0 \hfill \\ \Rightarrow x - \dfrac{\pi }{4} = k\pi \hfill \\ \Rightarrow x = \dfrac{\pi }{4} + k\pi ,\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}

Vậy phương trình lượng giác có nghiệm là x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)

Cách 3: Giải phương trình theo cos x

sin x = cos x

\begin{matrix} \Rightarrow \sin x - \cos x = 0 \hfill \\ \Rightarrow - \sqrt 2 \cos \left( {x + \dfrac{\pi }{4}} \right) = 0 \hfill \\ \Rightarrow \cos \left( {x + \dfrac{\pi }{4}} \right) = 0 \hfill \\ \Rightarrow x + \dfrac{\pi }{4} = \dfrac{\pi }{2} + k\pi \hfill \\ \Rightarrow x = \dfrac{\pi }{2} - \dfrac{\pi }{4} + k\pi \hfill \\ \Rightarrow x = \dfrac{\pi }{4} + k\pi ,\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}

Vậy phương trình lượng giác có nghiệm là x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)

C. Tập xác định của hàm số y = sin x – cos x

Tập xác định D = R

D. Xét tính chẵn lẻ của hàm số y = sin x – cos x

Ta có:

Với x thuộc D ⇒ – x thuộc D

Ta có: y = f(x) = sin x – cos x

⇒ f(– x) = sin (– x) – cos (– x) = – sin x – cos x

⇒ f(x) ≠ f(– x)

Vậy hàm số y = sin x – cos x không chẵn, không lẻ

E. GTLN, GTNN của hàm số y = sin x – cos x

Ta có: y = sin x – cos x

\begin{matrix} = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right) \hfill \\ - 1 \leqslant \sin x \leqslant 1 \hfill \\ \Rightarrow - \sqrt 2 \leqslant \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right) \leqslant \sqrt 2 \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\max y = \sqrt 2 } \\ {\min y = - \sqrt 2 } \end{array}} \right. \hfill \\ \end{matrix}

F. Đồ thị hàm số y = sin x – cos x

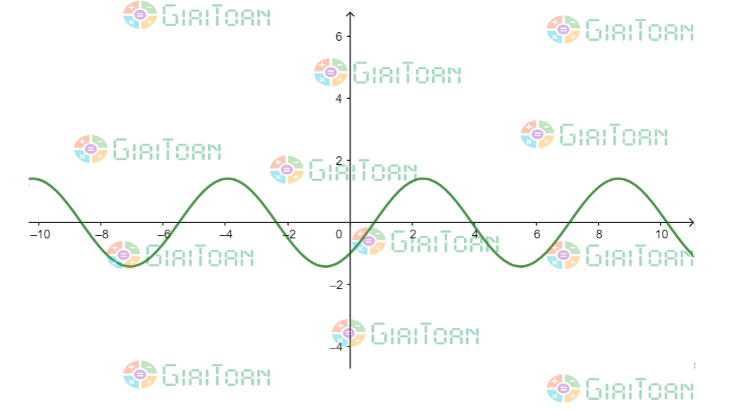
Sinx = cosx

G. Phương trình lượng giác thường gặp

• sin 2x + cos 2x = 1

• sin 2x + cos 2x = 0

• Sin x = 0

• Cos x = 0

• sin x + cos x = 1

• sin6 x + cos6 x = 1

• sin4 x + cos4 x = 1

--------------------------------------

Hi vọng Giải phương trình lượng giác thường gặp là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình lớp 11 cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Một số tài liệu liên quan:

Chia sẻ bởi: Thùy Chi
Mời bạn đánh giá!
  • Lượt xem: 53.985
Tìm thêm: Toán 11 Chuyên đề Toán 11
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần