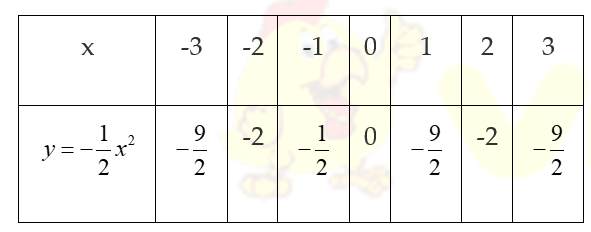Giaitoan.com Toán 9 Giải Toán 9 tập 2
Xử Nữ Giải Toán 9 tập 2Toán 9 Toán 9 Bài tập Toán 9

Bài toán yêu cầu tìm tích của một số dương với một số lớn hơn nó 2 đơn vị

, nhưng bạn Quân nhầm đầu bài lại tính tích của một số dương với một số bé hơn nó 2 đơn vị. Kết quả của bạn Quân là 120. Hỏi nếu làm đúng đầu bài đã cho thì kết quả phải là bao nhiêu?

2
Xóa Đăng nhập để viết
2 Câu trả lời
  • Thùy Chi
    Thùy Chi

    Lời giải chi tiết

    Gọi số mà đề bài đã cho là x; (điều kiện )

    Bạn Quân đã chọn số x – 2 để nhân với x.

    Tích của hai số là 120 nên ta có phương trình:

    x.(x – 2) = 120

    => x2 – 2x – 120 = 0

    Ta có a = 1; b’ = -1; c = 120

    => Δ’ = 121 > 0

    => Phương trình có hai nghiệm phân biệt:

    {x_1} = \frac{{1 - \sqrt {121} }}{1} = - 10\left( {ktm} \right);{x_2} = \frac{{1 + \sqrt {121} }}{1} = 12\left( {tm} \right)

    Vậy số cần tìm là 12

    Tích cần tìm là 12 . 14 = 168

    0 Trả lời 04/05/22
    • Bảo Bình
      Bảo Bình

      Các bước giải bài toán bằng cách lập phương trình

      Để giải bài toán bằng cách lập phương trình ta làm theo các bước:

      Bước 1: Lập phương trình

      + Chọn ẩn và đặt điều kiện cho ẩn

      + Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.

      + Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

      Bước 2: Giải phương trình

      Bước 3: Đối chiếu điều kiện rồi kết luận.

      0 Trả lời 04/05/22
      Tìm thêm: Toán 9 Bài tập Toán 9
      Câu hỏi mới
      Danh mục
      Hỏi bài ngay thôi!
      ×

      Gửi câu hỏi/bài tập

      Thêm vào câu hỏi
      Đăng

      Giải Toán 9 tập 2

      • Toán 9 Bài 3 Giải hệ phương trình bằng phương pháp thế

        Giải Toán 9 bài 13 Trang 15 SGK Cách giải hệ phương trình với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

        Bài 13 trang 15 SGK Toán 9 tập 2

        Bài 13 (SGK trang 15): Giải các hệ phương trình sau bằng phương pháp thế:

        a. \left\{ \begin{matrix} 3x-2y=11 \\ 4x-5y=3 \\ \end{matrix} \right.b. \left\{ \begin{matrix} \dfrac{x}{2}-\dfrac{y}{3}=1 \\ 5x-8y=3 \\ \end{matrix} \right.


        Hướng dẫn giải

        Bước 1. Rút x hoặc y từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

        Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

        Lời giải chi tiết

        a. \left\{ \begin{matrix} 3x-2y=11 \\ 4x-5y=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{11+2y}{3} \\ 4x-5y=3 \\ \end{matrix}\Leftrightarrow \right.\left\{ \begin{matrix} x=\dfrac{11+2y}{3} \\ 4.\dfrac{11+2y}{3}-5y=3 \\ \end{matrix}\Leftrightarrow \right.\left\{ \begin{matrix} x=\dfrac{11+2y}{3} \\ \dfrac{-7}{3}y+\dfrac{44}{3}=3 \\ \end{matrix} \right.

        \Leftrightarrow \left\{ \begin{matrix} x=\dfrac{11+2y}{3} \\ \dfrac{-7}{3}y+\dfrac{44}{3}=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=7 \\ y=5 \\ \end{matrix} \right.

        Vậy hệ phương trình có nghiệm duy nhất \left( x;y \right)=\left( 7;5 \right)

        b. \left\{ \begin{matrix} \dfrac{x}{2}-\dfrac{y}{3}=1 \\ 5x-8y=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} \dfrac{x}{2}=\dfrac{y}{3}+1 \\ 5x-8y=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{2}{3}y+2 \\ 5x-8y=3 \\ \end{matrix} \right.

        \begin{align} & \Leftrightarrow \left\{ \begin{matrix} x=\dfrac{2}{3}y+2 \\ 5.\left( \dfrac{2}{3}y+2 \right)-8y=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{2}{3}y+2 \\ -\dfrac{14}{3}y+10=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{2}{3}y+2 \\ y=\dfrac{3}{2} \\ \end{matrix} \right. \\ & \Leftrightarrow \left\{ \begin{matrix} x=3 \\ y=\dfrac{3}{2} \\ \end{matrix} \right. \\ \end{align}

        Vậy hệ phương trình có nghiệm duy nhất \left( x;y \right)=\left( 3;\frac{3}{2} \right)

        -----------------------------------------------------------

        Trên đây GiaiToan đã chia sẻ Giải Toán 9: Giải hệ phương trình bằng phương pháp thế. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!

        Ngày hỏi: 10:03 21/01

      • Toán 9 Bài 3 Giải hệ phương trình bằng phương pháp thế

        Giải Toán 9 Câu hỏi 1 Trang 14 SGK Cách giải hệ phương trình với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

        Câu hỏi 1 trang 14 SGK Toán 9 tập 2

        Câu hỏi 1 (SGK trang 14): Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)

        \left\{ \begin{matrix} 4x-5y=3 \\ 3x-y=16 \\ \end{matrix} \right.

        Lời giải chi tiết

        Ta biểu diễn y theo x từ phương trình thứ hai ta có:

        \left\{ \begin{matrix} 4x-5y=3 \\ 3x-y=16 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 4x-5y=3 \\ y=3x-16 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 4x-5.\left( 3x-16 \right)=3 \\ y=3x-16 \\ \end{matrix} \right.

        \Leftrightarrow \left\{ \begin{matrix} -11x+80=3 \\ y=3x-16 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=7 \\ y=5 \\ \end{matrix} \right.

        Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7; 5)

        ---> Bài liên quan: Giải Toán 9 Bài 3 Giải hệ phương trình bằng phương pháp thế

        ---> Câu hỏi tiếp theo:

        -----------------------------------------------------------

        Trên đây GiaiToan đã chia sẻ Giải Toán 9: Giải hệ phương trình bằng phương pháp thế. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!

        Ngày hỏi: 06:04 12/01

      • Toán 9 Bài 2: Đồ thị của hàm số y = ax^2 (a ≠ 0)

        Giải Toán 9 Bài 5 Trang 37 SGK Toán 9 tập 2 với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

        Bài 5 trang 37 SGK Toán 9 tập 2

        Bài 5 (SGK trang 37): Cho ba hàm số: y = \frac{1}{2}{x^2};y = {x^2};y = 2{x^2}

        a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

        b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

        c) Tìm ba điểm A’; B’; C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’; B và B’; C và C’.

        d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.

        Hướng dẫn giải

        Cách vẽ đồ thị hàm số y = ax2

        Bước 1: Xác định các điểm (1;a) và (2;4a) và các điểm đối xứng của chúng qua Oy.

        Bước 2: Vẽ parabol đi qua gốc O(0;0) và các điểm trên đồ thị.

        - Thay hoành độ x = x0 vào hàm số y = ax2 ta tìm được tung độ y tương ứng.

        - Áp dụng tính chất: Nếu a > 0 thì đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.

        Lời giải chi tiết

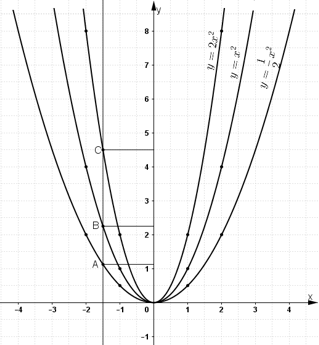
        a. Vẽ đồ thị:

        Trên mặt phẳng lưới lấy các điểm (-2; 2); (-1; \frac{1}{2}); (0; 0); (1; 1/2); (2; 2), nối chúng thành một đường cong ta được đồ thị hàm số y = \frac{1}{2}{x^2}

        Lấy các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4), nối chúng thành một đường cong ta được đồ thị hàm số y = x2

        Lấy các điểm (-2; 8); (-1; 2); (0; 0); (1; 2); (2; 8), nối chúng thành một đường cong ta được đồ thị hàm số y = 2x2

        Bài 5 trang 37 SGK Toán 9 tập 2

        b) Lấy các điểm A, B, C lần lượt nằm trên 3 đồ thị và có hoành độ bằng -1,5.

        Từ điểm (-1,5;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị y = \frac{1}{2}{x^2};y = {x^2};y = 2{x^2} lần lượt tại các điểm A, B, C.

        Gọi {y_A};{y_B};{y_C} lần lượt là tung độ của các điểm A, B, C. Ta có:

        \begin{matrix} {y_A} = \dfrac{1}{2}{\left( { - 1,5} \right)^2} = \dfrac{9}{8} \hfill \\ {y_B} = {\left( { - 1,5} \right)^2} = \dfrac{9}{4} \hfill \\ {y_C} = 2.{\left( { - 1,5} \right)^2} = \dfrac{9}{2} \hfill \\ \end{matrix}

        Bài 5 trang 37 SGK Toán 9 tập 2

        Khi đó tung độ điểm A bằng \frac{9}{8}; tung độ điểm B bằng \frac{9}{4}; tung độ điểm C bằng \frac{9}{2}

        c)

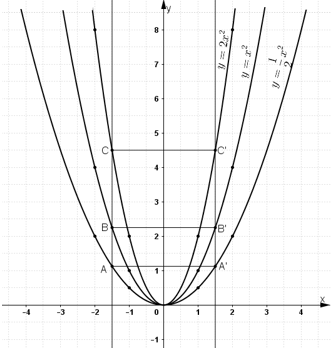
        Bài 5 trang 37 SGK Toán 9 tập 2

        Lấy các điểm A’, B’, C’ lần lượt nằm trên 3 đồ thị và có hoành độ bằng \frac{3}{2}

        Từ điểm (\frac{3}{2} ;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị y = \frac{1}{2}{x^2};y = {x^2};y = 2{x^2} lần lượt tại các điểm A, B, C.

        Gọi {y_A};{y_B};{y_C} lần lượt là tung độ của các điểm A, B, C. Ta có:

        \begin{matrix} {y_A} = \dfrac{1}{2}{\left( { - 1,5} \right)^2} = \dfrac{9}{8} \hfill \\ {y_B} = {\left( { - 1,5} \right)^2} = \dfrac{9}{4} \hfill \\ {y_C} = 2.{\left( { - 1,5} \right)^2} = \dfrac{9}{2} \hfill \\ \end{matrix}

        Khi đó A'\left( {\frac{3}{2};\frac{9}{8}} \right);B'\left( {\frac{3}{2};\frac{9}{4}} \right);C'\left( {\frac{3}{2};\frac{9}{2}} \right)

        Nhận xét: A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy.

        d) Hàm số có giá trị nhỏ nhất ⇔ y nhỏ nhất.

        Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).

        Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.

        -----------------------------------------------------------

        Trên đây GiaiToan đã chia sẻ Giải Toán 9: Đồ thị của hàm số bậc 2. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!

        Ngày hỏi: 16:03 16/12

      • Câu hỏi 3 trang 45 SGK Toán 9

        Câu hỏi 3 trang 45 SGK Toán 9 tập 2 Công thức nghiệm của phương trình bậc hai với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9. Tài liệu được biên soạn và đăng tải với hướng dẫn chi tiết các bài tập tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Chúc các bạn học tập tốt!

        Giải Câu hỏi 3 Toán 9 trang 45

        Câu hỏi 3 (trang 45 SGK): Áp dụng công thức nghiệm để giải các phương trình:

        a) 5x2 – x + 2 = 0

        b) 4x2 – 4x + 1 = 0

        c) -3x2 + x + 5 = 0

        Hướng dẫn giải

        Đối với phương trình bậc hai có dạng ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac

        + Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt

        {x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}

        + Nếu ∆ = 0 thì phương trình có nghiệm kép {x_1} = {x_2} = - \frac{b}{{2a}}

        + Nếu ∆ < 0 thì phương trình vô nghiệm

        Lời giải chi tiết

        a) 5x2 – x + 2 = 0

        Ta có a = 5; b = -1; c = 2

        Tính biệt thức ∆ ta có:

        ∆ = (-1)2 – 4.5.2 = -39 < 0

        => Phương trình vô nghiệm.

        b) 4x2 – 4x + 1 = 0

        Ta có a = 4; b = -4; c = 1

        Tính biệt thức ∆ ta có:

        ∆ = (-4)2 – 4.4.1 = 0

        => Phương trình có nghiệm kép

        => {x_1} = {x_2} = \frac{{ - \left( { - 4} \right)}}{{2.4}} = \frac{1}{2}

        c) -3x2 + x + 5 = 0

        Ta có a = -3; b = 1; c = 5

        Tính biệt thức ∆ ta có:

        ∆ = 12 + 4.3.5 = 61 > 0

        => Phương trình có hai nghiệm phân biệt

        => \sqrt \Delta = \sqrt {61}

        => {x_1} = \frac{{ - 1 + \sqrt {61} }}{{2.\left( { - 3} \right)}} = \frac{{ - 1 + \sqrt {61} }}{{ - 6}};{x_2} = \frac{{ - 1 - \sqrt {61} }}{{2.\left( { - 3} \right)}} = \frac{{ - 1 - \sqrt {61} }}{{ - 6}} = \frac{{1 + \sqrt {61} }}{6}

        Câu hỏi cùng bài:

        Bài tiếp theo: Bài 5: Công thức nghiệm thu gọn

        -----------------------------------------------------

        Trên đây là lời giải chi tiết Câu hỏi 3 trang 45 SGK Toán 9 tập 2 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 4 Hàm số y = ax^2 (a ≠ 0) Phương trình bậc hai một ẩn. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 9. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!

        Ngày hỏi: 04:03 02/12

      • Toán 9 Bài 3 Giải hệ phương trình bằng phương pháp thế

        Giải Toán 9 bài 12 Trang 15 SGK Cách giải hệ phương trình với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

        Bài 12 trang 15 SGK Toán 9 tập 2

        Bài 12 (SGK trang 15): Giải các hệ phương trình sau bằng phương pháp thế:

        a. \left\{ \begin{matrix} x-y=3 \\ 3x-4y=2 \\ \end{matrix} \right.b. \left\{ \begin{matrix} 7x-3y=5 \\ 4x+y=2 \\ \end{matrix} \right.c. \left\{ \begin{matrix} x+3y=-2 \\ 5x-4y=11 \\ \end{matrix} \right.

        Hướng dẫn giải

        Bước 1. Rút x hoặc y từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

        Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

        Lời giải chi tiết

        a. \left\{ \begin{matrix} x-y=3 \\ 3x-4y=2 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=y+3 \\ 3x-4y=2 \\ \end{matrix}\Leftrightarrow \right.\left\{ \begin{matrix} x=y+3 \\ 3.\left( y+3 \right)-4y=2 \\ \end{matrix} \right.

        \Leftrightarrow \left\{ \begin{matrix} x=y+3 \\ -y+9=2 \\ \end{matrix}\Leftrightarrow \right.\left\{ \begin{matrix} x=y+3 \\ y=7 \\ \end{matrix}\Leftrightarrow \right.\left\{ \begin{matrix} x=10 \\ y=7 \\ \end{matrix} \right.

        Vậy hệ phương trình có nghiệm duy nhất \left( x;y \right)=\left( 10;7 \right)

        b. \left\{ \begin{matrix} 7x-3y=5 \\ 4x+y=2 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 7x-3y=5 \\ y=2-4x \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 7x-3.\left( 2-4x \right)=5 \\ y=2-4x \\ \end{matrix} \right.

        \Leftrightarrow \left\{ \begin{matrix} 19x-6=5 \\ y=2-4x \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{11}{19} \\ y=2-4x \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{11}{19} \\ y=\dfrac{-6}{19} \\ \end{matrix} \right.

        Vậy hệ phương trình có nghiệm duy nhất \left( x;y \right)=\left( \frac{11}{19};-\frac{6}{19} \right)

        c. \left\{ \begin{matrix} x+3y=-2 \\ 5x-4y=11 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=-2-3y \\ 5x-4y=11 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=-2-3y \\ 5.\left( -2-3y \right)-4y=11 \\ \end{matrix} \right.

        \Leftrightarrow \left\{ \begin{matrix} x=-2-y \\ -19y-10=11 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=-2-y \\ -19y-10=11 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=-2-y \\ y=\dfrac{-21}{19} \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=\dfrac{25}{19} \\ y=\dfrac{-21}{19} \\ \end{matrix} \right.

        Vậy hệ phương trình có nghiệm duy nhất \left( x;y \right)=\left( \frac{25}{19};-\frac{21}{19} \right)

        -----------------------------------------------------------

        Trên đây GiaiToan đã chia sẻ Giải Toán 9: Giải hệ phương trình bằng phương pháp thế. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!

        Ngày hỏi: 18:03 25/11

      • Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0)

        Giải Toán 9 Câu hỏi 4 Trang 30 SGK Toán 9 tập 2 với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

        Câu hỏi 4 trang 30 SGK Toán 9 tập 2

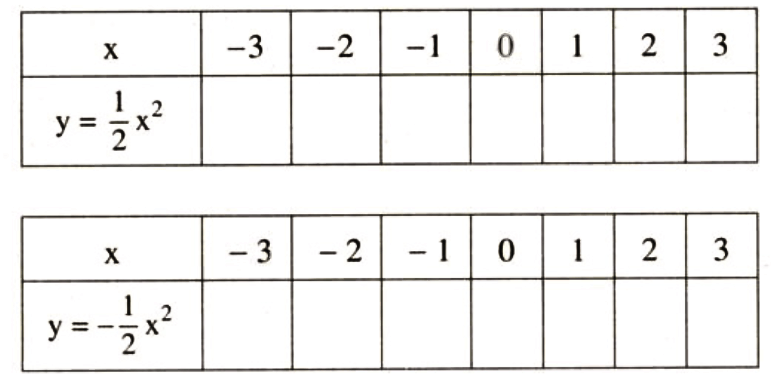
        Câu hỏi 4 (SGK trang 30): Cho hai hàm số y = \frac{1}{2}{x^2} và y = - \frac{1}{2}{x^2}. Tính các giá trị tương ứng của y rồi điền vào các ô trống tương ứng ở hai bảng sau; kiểm nghiệm lại nhận xét nói trên:

        Câu hỏi 4 trang 30 SGK Toán 9 tập 2

        Hướng dẫn giải

        Thay từng giá trị của x vào hàm số tương ứng.

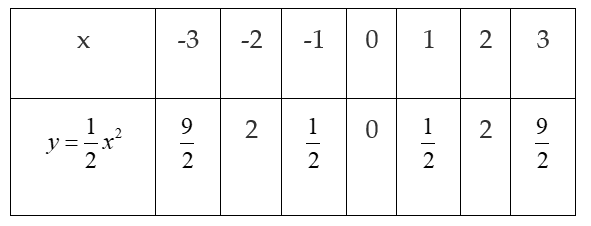
        Lời giải chi tiết

        Câu hỏi 4 trang 30 SGK Toán 9 tập 2

        Câu hỏi 4 trang 30 SGK Toán 9 tập 2

        Bài liên quan: Giải Toán 9 Bài 1 Hàm số y = ax^2 (a ≠ 0)

        Câu hỏi cùng bài: 

        Bài tiếp theo: Giải Toán 9 Bài 2 Đồ thị của hàm số y = ax^2 (a ≠ 0)

        -----------------------------------------------------------

        Trên đây GiaiToan đã chia sẻ Giải Toán 9: Hàm số bậc 2. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!

        Ngày hỏi: 16:03 15/10
      Xem thêm