Bài 5 trang 37 SGK Toán 9 tập 2

Giải SGK Toán 9

1 Đánh giá

Toán 9 Bài 2: Đồ thị của hàm số y = ax^2 (a ≠ 0)

Giải Toán 9 Bài 5 Trang 37 SGK Toán 9 tập 2 với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 5 trang 37 SGK Toán 9 tập 2

Bài 5 (SGK trang 37): Cho ba hàm số: $y = \frac{1}{2}{x^2};y = {x^2};y = 2{x^2}$

a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

c) Tìm ba điểm A’; B’; C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’; B và B’; C và C’.

d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.

Hướng dẫn giải

Cách vẽ đồ thị hàm số y = ax²

Bước 1: Xác định các điểm (1;a) và (2;4a) và các điểm đối xứng của chúng qua Oy.

Bước 2: Vẽ parabol đi qua gốc O(0;0) và các điểm trên đồ thị.

- Thay hoành độ x = x₀ vào hàm số y = ax² ta tìm được tung độ y tương ứng.

- Áp dụng tính chất: Nếu a > 0 thì đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.

Lời giải chi tiết

a. Vẽ đồ thị:

Trên mặt phẳng lưới lấy các điểm (-2; 2); (-1; $\frac{1}{2}$ ); (0; 0); (1; 1/2); (2; 2), nối chúng thành một đường cong ta được đồ thị hàm số $y = \frac{1}{2}{x^2}$

Lấy các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4), nối chúng thành một đường cong ta được đồ thị hàm số y = x²

Lấy các điểm (-2; 8); (-1; 2); (0; 0); (1; 2); (2; 8), nối chúng thành một đường cong ta được đồ thị hàm số y = 2x²

Bài 5 trang 37 SGK Toán 9 tập 2

b) Lấy các điểm A, B, C lần lượt nằm trên 3 đồ thị và có hoành độ bằng -1,5.

Từ điểm (-1,5;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị $y = \frac{1}{2}{x^2};y = {x^2};y = 2{x^2}$ lần lượt tại các điểm A, B, C.

Gọi ${y_A};{y_B};{y_C}$ lần lượt là tung độ của các điểm A, B, C. Ta có:

$\begin{matrix} {y_A} = \dfrac{1}{2}{\left( { - 1,5} \right)^2} = \dfrac{9}{8} \hfill \\ {y_B} = {\left( { - 1,5} \right)^2} = \dfrac{9}{4} \hfill \\ {y_C} = 2.{\left( { - 1,5} \right)^2} = \dfrac{9}{2} \hfill \\ \end{matrix}$

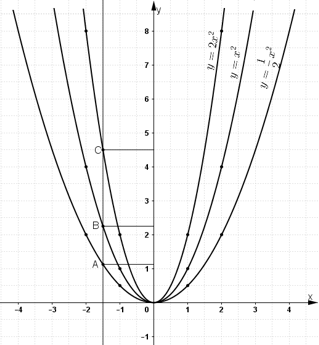
Bài 5 trang 37 SGK Toán 9 tập 2

Khi đó tung độ điểm A bằng $\frac{9}{8}$ ; tung độ điểm B bằng $\frac{9}{4}$ ; tung độ điểm C bằng $\frac{9}{2}$

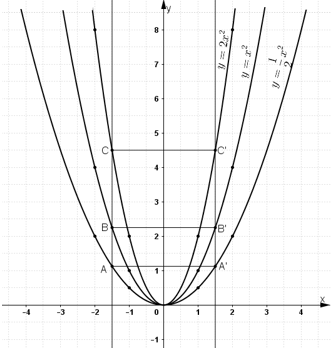
Bài 5 trang 37 SGK Toán 9 tập 2

Lấy các điểm A’, B’, C’ lần lượt nằm trên 3 đồ thị và có hoành độ bằng $\frac{3}{2}$

Từ điểm ( $\frac{3}{2}$ ;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị $y = \frac{1}{2}{x^2};y = {x^2};y = 2{x^2}$ lần lượt tại các điểm A, B, C.

Gọi ${y_A};{y_B};{y_C}$ lần lượt là tung độ của các điểm A, B, C. Ta có:

Khi đó $A'\left( {\frac{3}{2};\frac{9}{8}} \right);B'\left( {\frac{3}{2};\frac{9}{4}} \right);C'\left( {\frac{3}{2};\frac{9}{2}} \right)$

Nhận xét: A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy.

d) Hàm số có giá trị nhỏ nhất ⇔ y nhỏ nhất.

Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).

Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9: Đồ thị của hàm số bậc 2. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!