Toán 10 Bài 17: Dấu của tam thức bậc hai Toán 10 bài 17 Sách Kết nối tri thức

1 Đánh giá

Lý thuyết Toán 10 KNTT bài 16

1. Dấu của tam thức bậc hai
2. Bất phương trình bậc hai

GiaiToan mời các bạn cùng tham khảo nội dung bài Lý thuyết Toán 10 KNTT bài 17 nhằm nắm vững kiến thức trọng tâm về dấu của tam thức bậc hai và học tốt môn Toán lớp 10.

1. Dấu của tam thức bậc hai

Tam thức bậc hai (đối với x) là biểu thức có dạng ax² + bx + c, trong đó a, b, c là những số thực cho trước (với $a \ne 0$ ), được gọi là các hệ số của tam thức bậc hai.

Người ta thường viết f(x) = ax² + bx + c. Các đa thức đã cho A = $0,5x^{2}$ , B = $1-x^{2}$ , C = $x^{2}+x+1$ , D = (1-x)(2x+1) là những tam thức bậc hai. Ở đa thức A, ta có ; a = 0,5; b = 0, c = 0.

Chú ý: Nghiệm của phương trình bậc hai ax2 + bx + c = 0 cũng được gọi là nghiệm của tam thức bậc hai ax² + bx + c.

Lý thuyết Toán 10 KNTT bài 17

Cho tam thức bậc hai f(x) = ax²+ bx + c $a \ne 0$ .

+ Nếu $\Delta < 0$ thì f(x) cùng dẫu với hệ số a với mọi $x \in R$ .

+ Nếu $\Delta = 0$ thì f(x) cùng dấu với hệ số a với mọi $x \ne - \frac{b}{{2{\rm{a}}}}$ và $f\left( { - \frac{b}{{2{\rm{a}}}}} \right) = 0$ .

+ Nếu $\Delta > 0$ thi tam thức f(x) có hai nghiệm phân biệt x1 và x2 $\left( {{x_1} < {x_2}} \right)$ . Khi đó f(x) cùng dấu với hệ số a với mọi $x \in \left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)$ ; f(x) trái dấu với hệ số a với mọi $x \in \left( {{x_1};{x_2}} \right)$ .

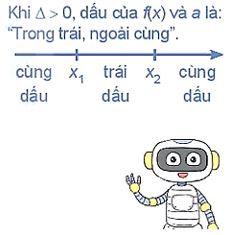
Chú ý: Trong Định lí về dấu tam thức bậc hai có thể thay $\Delta bởi \Delta '$ .

Ví dụ: Xét dâu các tam thức bậc hai sau:

a) ${x^2} + x + 1$
b) $- \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}$
c) $2{x^2} + 6x - 8$

Giải

a) $(f(x) = {x^2} + x + 1$ có $\Delta = -3 < 0$ và a = 1 > 0 nên f(x) > 0 với mọi $x \in R$ .

b) $g(x) = - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}$ có $\Delta = 0$ và $a = - \frac{3}{2} > 0$ nên g(x) có nghiệm kép x = 3 và g(x) < 0 với mọi $x \ne 3$ .

c) Dễ thấy $h(x) = 2{x^2} + 6x - 8$ có $\Delta '$ = 25 > 0,a = 2 > 0\) và có hai nghiệm phân biệt ${x_1} = - 4;{x_2} = 1$ .

Do đó ta có bẳng xét dấu h(x)

Lý thuyết Toán 10 KNTT bài 17

Suy ra h(x) > 0 với mọi $x \in \left( { - \infty ; - 4} \right) \cup \left( {1; + \infty } \right)$ và h(x) < 0 với mọi $x \in \left( { - 4;1} \right)$ .

2. Bất phương trình bậc hai

+ Bất phương trình bậc hai ẩn x là bất phương trình có dạng ax²+ bx + c > 0 (hoặc ax²+ bx + c > 0, ax²+ bx + c < 0, $a{x^2} + bx + c \le 0$ , trong đó a, b, c là những số thực đã cho và $a \ne 0$ .

+ Số thực x₀ gọi là một nghiệm của bất phương trình bậc hai ax²+ bx + c > 0, nếu ax²+ bx + c > 0. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax²+ bx + c > 0 gọi là tập nghiệm của bắt phương trình này.

+ Giải bất phương trình bậc hai f(x)= ax²+ bx + c > 0 là tìm tập nghiệm của nó, tức là tìm các khoảng mà trong đó f(x) cùng dấu với hệ số a (nếu a > 0) hay trái dầu với hệ số a (nếu a < 0).

Nhận xét: Để giải bất phương trình bậc hai ax²+ bx + c > 0 (hoặc $a{x^2} + bx + c \ge 0, ax2+ bx + c < 0, a{x^2} + bx + c \le 0$ ) ta cần xét dấu tam thức ax²+ bx + c, từ đó suy ra tập nghiệm.

Ví dụ: Giải các bất phương trình sau:

a) $3{x^2} + x + 5 \le 0\\$
b) $- 3{x^2} + 2\sqrt 3 - 1 \ge 0\\$
c) $- {x^2} + 2x + 1 > 0$

Giải

a) Tam thức $f(x) = 3{x^2} + x + 5$ có $\Delta = - 59 < 0$ , hệ số a = 3 > 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là 3x² + x + 5 > 0) với mọi $x \in R$ . Suy ra bất phường trình vô nghiệm.

b) Tam thức $f(x) = - 3{x^2} + 2\sqrt 3 - 1$ có $\Delta ' = 0$ , hệ số a = -3 < 0 nên f(x) luôn âm (cùng dấu với a) với mọi $x \ne \frac{{\sqrt 3 }}{3}$ , tức là $- 3{x^2} + 2\sqrt 3 - 1 < 0$ với mọi $x = \frac{{\sqrt 3 }}{3}$ .

Suy ra bất phương trình có nghiệm duy nhất $x = \frac{{\sqrt 3 }}{3}$ .

c) Tam thức $f(x) = - {x^2} + 2x + 1$ có $\Delta ' = 2 > 0$ nên f(x) có hai nghiệm ${x_1} = 1 - \sqrt 2 và {x_2} = 1 + \sqrt 2$

Mặt khác a = -1 < 0, do đó ta có bảng xét dấu sau:

Lý thuyết Toán 10 KNTT bài 17

Tập nghiệm của bất phương trình là $S = \left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)$

Toán 10 Kết nối tri thức Bài 17: Dấu của tam thức bậc hai được giáo viên GiaiToan tổng hợp và đăng tải nhằm hy vọng với phần lý thuyết này sẽ giúp các em nắm chắc kiến thức, từ đó áp dụng vào giải các bài tập Toán 10 đạt kết quả tốt. Tham khảo thêm các bài lý thuyết khác được đăng tải chi tiết bám sát chương trình học SGK Kết nối tri thức với cuộc sống tại Lý thuyết Toán 10 đồng thời tại chuyên mục Giải Toán 10 Kết nối tri thức Tập 2 có đầy đủ các bài tập do GiaiToan biên soạn để giúp bạn ôn tập nhé.